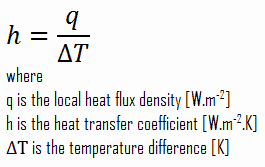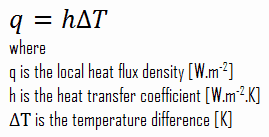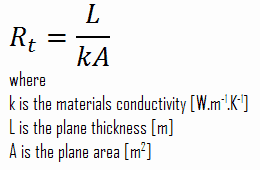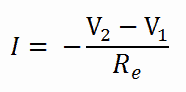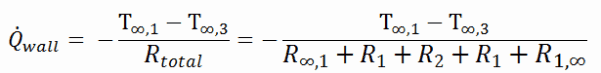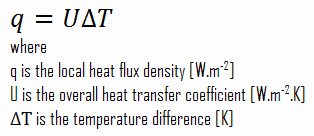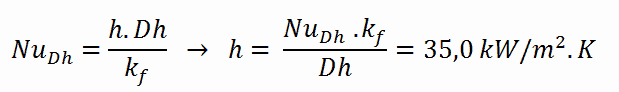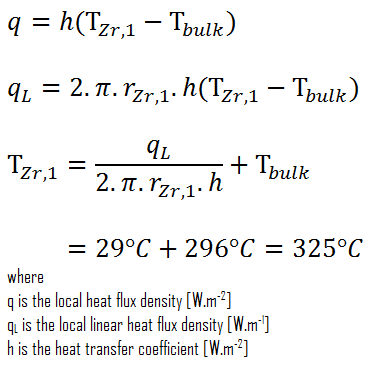The convective heat transfer coefficient, h, can be defined as:
The rate of heat transfer between a solid surface and a fluid per unit surface area per unit temperature difference.
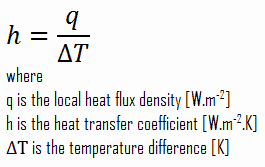
Newton’s Law of Cooling
Despite the complexity of convection, the rate of convection heat transfer is observed to be proportional to the temperature difference. It is conveniently expressed by Newton’s law of cooling, which states that:
The rate of heat loss of a body is directly proportional to the difference in the temperatures between the body, and its surroundings, provided the temperature difference is small, and the nature of radiating surface remains the same.
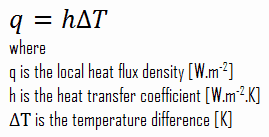
Note that ΔT is given by the surface or wall temperature, Twall, and the bulk temperature, T∞, which is the temperature of the fluid sufficiently far from the surface.
Convective Heat Transfer Coefficient
As can be seen, the constant of proportionality will be crucial in calculations, and it is known as the convective heat transfer coefficient, h. The convective heat transfer coefficient, h, can be defined as:
The rate of heat transfer between a solid surface and a fluid per unit surface area per unit temperature difference.
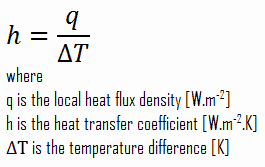
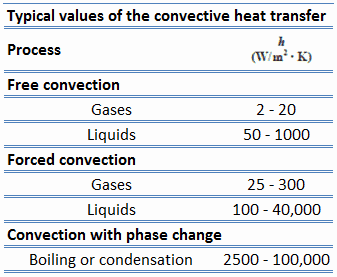 The convective heat transfer coefficient depends on the fluid’s physical properties and the physical situation. The convective heat transfer coefficient is not a property of the fluid. It is an experimentally determined parameter whose value depends on all the variables influencing convection, such as the surface geometry, the nature of fluid motion, the properties of the fluid, and the bulk fluid velocity.
The convective heat transfer coefficient depends on the fluid’s physical properties and the physical situation. The convective heat transfer coefficient is not a property of the fluid. It is an experimentally determined parameter whose value depends on all the variables influencing convection, such as the surface geometry, the nature of fluid motion, the properties of the fluid, and the bulk fluid velocity.
Typically, the convective heat transfer coefficient for laminar flow is relatively low compared to the convective heat transfer coefficient for turbulent flow. This is due to turbulent flow having a thinner stagnant fluid film layer on the heat transfer surface.
It must be noted this stagnant fluid film layer plays a crucial role in the convective heat transfer coefficient. It is observed that the fluid comes to a complete stop at the surface and assumes a zero velocity relative to the surface. This phenomenon is known as the no-slip condition, and therefore, at the surface, energy flow occurs purely by conduction. But in the next layers, both conduction and diffusion-mass movement occur at the molecular or macroscopic levels. Due to the mass movement, the rate of energy transfer is higher. As was written, nucleate boiling at the surface effectively disrupts this stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid.
A similar phenomenon occurs for the temperature. It is observed that the fluid’s temperature at the surface and the surface will have the same temperature at the point of contact. This phenomenon is known as the no-temperature-jump condition, and it is very important for the theory of nucleate boiling.
Values of the heat transfer coefficient, h, have been measured and tabulated for the commonly encountered fluids and flow situations occurring during heat transfer by convection.
Thermal Resistance - Analogy to Electric Resistance
See also:
Thermal ResistanceThermal resistance is a heat property and a temperature difference measurement by which an object or material resists a heat flow. The thermal resistance for conduction in a plane wall is defined as:
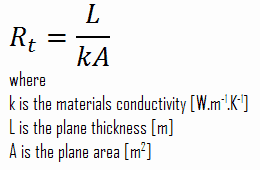
The equation above can also be derived for convective heat transfer. For heat flow is analogous to the relation for electric current flow I, expressed as:
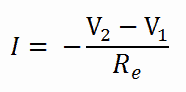
where Re = L/σeA is the electric resistance and V1 – V2 is the voltage difference across the resistance (σe is the electrical conductivity). The analogy between both equations is obvious. The heat transfer rate through a layer corresponds to the electric current, thermal resistance corresponds to electrical resistance, and temperature difference corresponds to the voltage difference across the layer. The temperature difference is the potential or driving function for the heat flow, resulting in the Fourier equation being written similarly to Ohm’s Law of Electrical Circuit Theory.
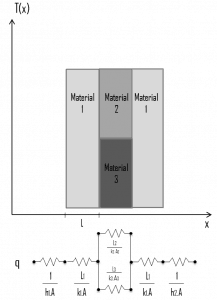 Circuit representations provide a useful tool for conceptualizing and quantifying heat transfer problems. This analogy can also be used for the thermal resistance of the surface against heat convection. Note that when the convection heat transfer coefficient is very large (h → infinity), the convection resistance becomes zero and the surface temperature approaches the bulk temperature. This situation is approached in practice at surfaces where intensive boiling and condensation occur.
Circuit representations provide a useful tool for conceptualizing and quantifying heat transfer problems. This analogy can also be used for the thermal resistance of the surface against heat convection. Note that when the convection heat transfer coefficient is very large (h → infinity), the convection resistance becomes zero and the surface temperature approaches the bulk temperature. This situation is approached in practice at surfaces where intensive boiling and condensation occur.
The heat transfer through the composite wall can be calculated from these resistances. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.
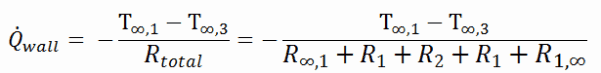
The equivalent thermal circuit for the plane wall with convection surface conditions is shown in the figure.
See also: Wiedemann–Franz Law
U-factor - Overall Heat Transfer Coefficient
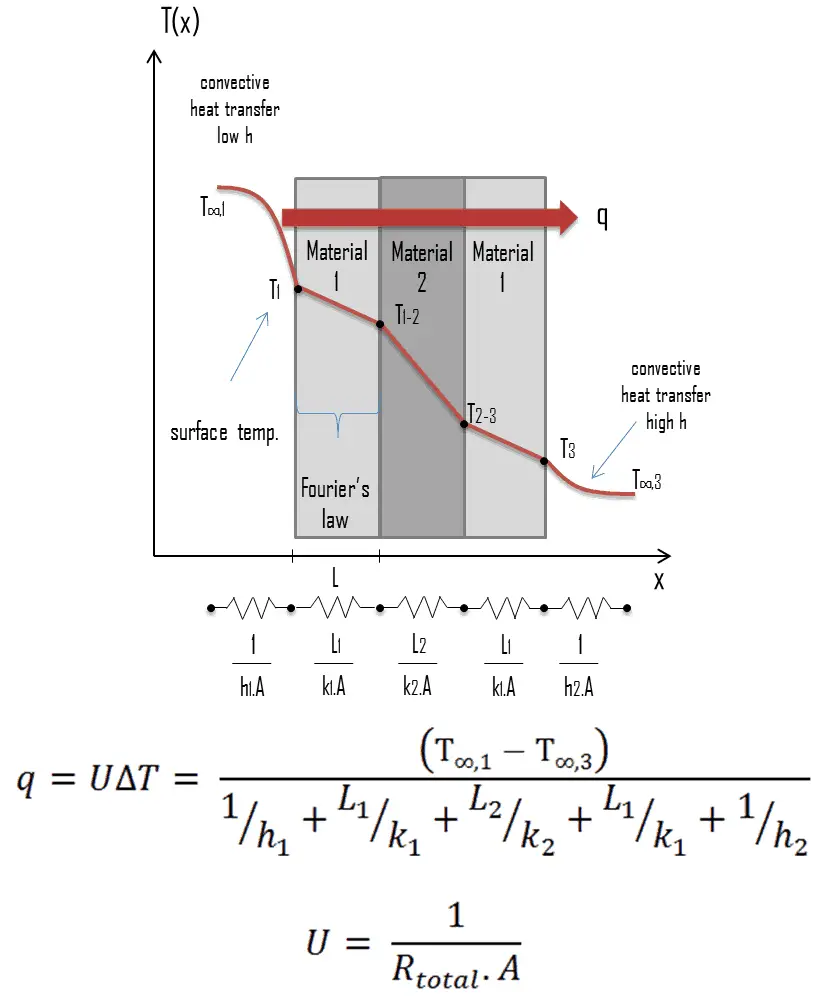
Many of the heat transfer processes encountered in industry involve composite systems and even involve a combination of both
conduction and
convection. It is often convenient to work with an
overall heat transfer coefficient, known as a
U-factor with these composite systems. The U-factor is defined by an expression analogous to
Newton’s law of cooling:
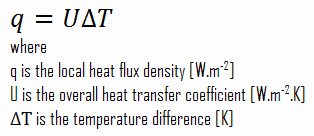
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem. For example, heat transfer in a steam generator involves convection from the bulk of the reactor coolant to the steam generator inner tube surface, conduction through the tube wall, and convection (boiling) from the outer tube surface to the secondary side fluid.
In cases of combined heat transfer for a heat exchanger, there are two values for h. The convective heat transfer coefficient (h) for the fluid film inside the tubes and a convective heat transfer coefficient for the fluid film outside the tubes. The thermal conductivity (k) and thickness (Δx) of the tube wall must also be accounted for.
Overall Heat Transfer Coefficient – Plane Wall
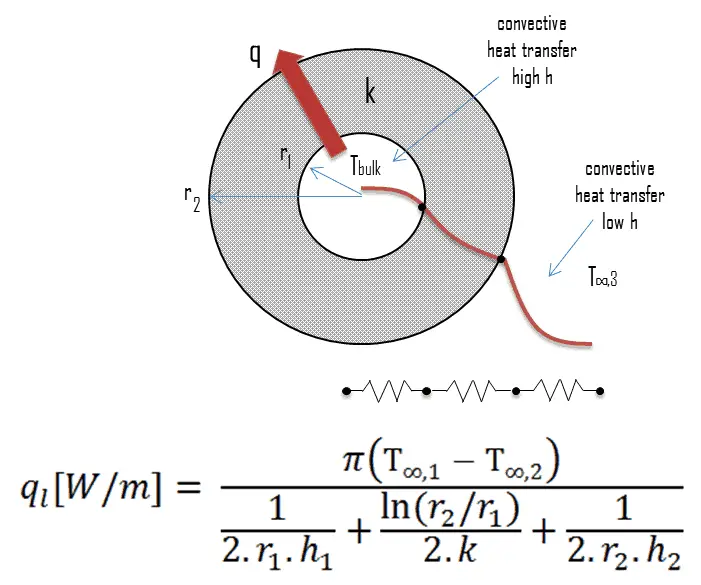
Overall Heat Transfer Coefficient – Cylindrical Tubes
Steady heat transfer through multilayered cylindrical or spherical shells can be handled just like multilayered plane walls.
Example: Convective Heat Transfer Coefficient
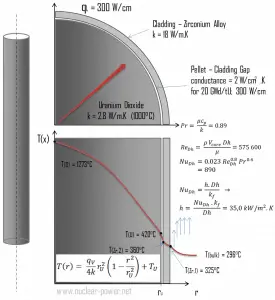 From: Example – Convective Heat Transfer
From: Example – Convective Heat Transfer
Detailed knowledge of geometry, fluid parameters, the outer radius of cladding, linear heat rate, convective heat transfer coefficient allows us to calculate the temperature difference ∆T between the coolant (Tbulk) and the cladding surface (TZr,1).
To calculate the cladding surface temperature, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the Nusselt number, which is NuDh = 890
- the hydraulic diameter of the fuel channel is Dh = 13,85 mm
- the thermal conductivity of reactor coolant (300°C) is: kH2O = 0.545 W/m.K
- the bulk temperature of reactor coolant at this axial coordinate is Tbulk = 296°C
- the linear heat rate of the fuel is: qL = 300 W/cm (FQ ≈ 2.0)
The convective heat transfer coefficient, h, is given directly by the definition of Nusselt number:
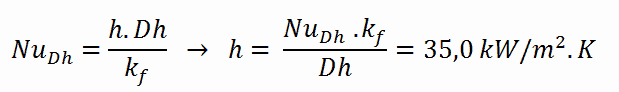
Finally, we can calculate the cladding surface temperature (TZr,1) simply using Newton’s Law of Cooling:
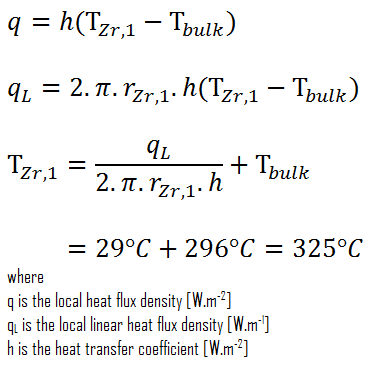
For PWRs at normal operation, there is compressed liquid water inside the reactor core, loops, and steam generators. The pressure is maintained at approximately 16MPa. At this pressure, water boils at approximately 350°C(662°F). As can be seen, the surface temperature TZr,1 = 325°C ensures that even subcooled boiling does not occur. Note that subcooled boiling requires TZr,1 = Tsat. Since the inlet temperatures of the water are usually about 290°C (554°F), it is obvious this example corresponds to the lower part of the core. At higher core elevations, the bulk temperature may reach up to 330°C. The temperature difference of 29°C causes the subcooled boiling may occur (330°C + 29°C > 350°C). On the other hand, nucleate boiling at the surface effectively disrupts the stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid. As a result, the convective heat transfer coefficient significantly increases, and therefore at higher elevations, the temperature difference (TZr,1 – Tbulk) significantly decreases.
References:
Heat Transfer:- Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
- U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
- Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.
 The convective heat transfer coefficient depends on the fluid’s physical properties and the physical situation. The convective heat transfer coefficient is not a property of the fluid. It is an experimentally determined parameter whose value depends on all the variables influencing convection, such as the surface geometry, the nature of fluid motion, the properties of the fluid, and the bulk fluid velocity.
The convective heat transfer coefficient depends on the fluid’s physical properties and the physical situation. The convective heat transfer coefficient is not a property of the fluid. It is an experimentally determined parameter whose value depends on all the variables influencing convection, such as the surface geometry, the nature of fluid motion, the properties of the fluid, and the bulk fluid velocity. From: Example – Convective Heat Transfer
From: Example – Convective Heat Transfer