Facebook Instagram Youtube Twitter

Delayed Neutrons Fraction

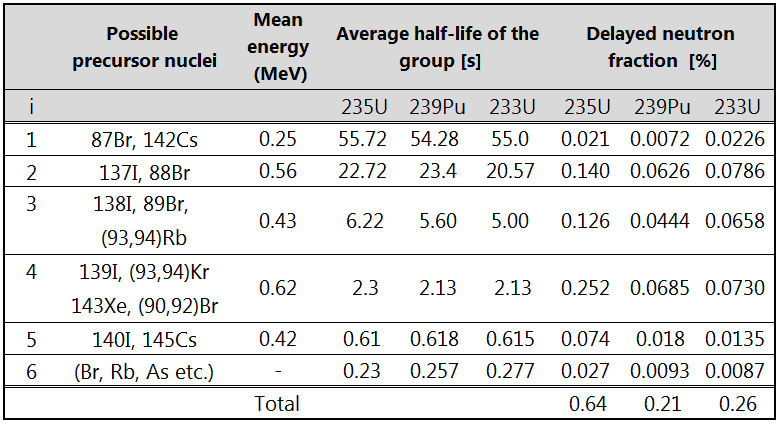
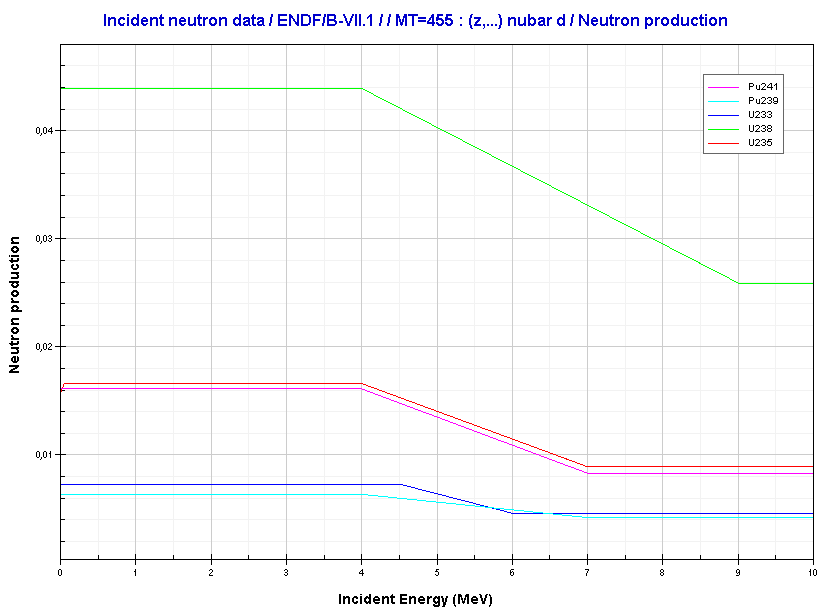
Delayed Neutrons Fraction

The total yield of delayed neutrons per fission, vd, depends on:

  • An isotope that is fissioned (see table).
  • The energy of a neutron induces fission (see chart).
 
Table: Six Groups of Precursors
Parameters of Delayed Neutrons
Delayed neutrons are traditionally represented by six delayed neutron groups, whose yields and decay constants (λ) are obtained from nonlinear least-squares fits to experimental measurements.
Chart: Delayed Neutron Production - MT-455
Delayed Neutron Production
This chart shows the energy dependency of delayed neutrons production. The delayed neutrons production remains constant to 4 MeV, then a linear decrease is observed. Source: JANIS (Java-based Nuclear Data Information Software); ENDF/B-VII.1
In reactor kinetic calculations it is convenient to use relative units usually referred to as delayed neutron fraction (DNF). At the steady-state condition of criticality, with keff = 1, the delayed neutron fraction is equal to the precursor yield fraction (β).delayed neutron fraction - definitionwhere βi is defined as the fraction of the neutrons which appear as delayed neutrons in the ith group. In contrast to the prompt neutrons emitted with a continuous energy spectrum, the delayed neutrons in each group appear with a more or less well-defined energy. In general, the delayed neutrons are emitted with much less energy than the most prompt neutrons. The distinction between these two parameters is obvious. The delayed neutron fraction is dependent on the certain reactivity of the multiplying system. On the other hand, β is not dependent on reactivity. These two factors, DNF and β, are not the same things in case of a rapid change in the number of neutrons in the reactor.

In LWRs, the delayed neutron fraction decreases with fuel burnup. This is due to isotopic changes in the fuel. It is simple. Fresh uranium fuel contains only 235U as the fissile material. Meanwhile, during fuel burnup, the importance of fission of 239Pu increases (in some cases up to 50%). Since 239Pu produces significantly less delayed neutrons, the resultant core delayed neutron fraction of a multiplying system decreases (the weighted average of the constituent delayed neutron fractions). This is also the reason why the neutron spectrum in the core becomes harder with fuel burnup.

βcore= ∑ Pi.βi

where Pi is fraction of power generated by isotope i.

Example:Let say the reactor is at the beginning of the cycle and approximately 98% of reactor power is generated by 235U fission and 2% by 238U fission as a result of fast fission. Calculate the core delayed neutron fraction.

βcore= ∑ Pi.βi = 0.98 x β235 + 0.02 x β238

= 0.98 x 0.0065 + 0.02 x 0.0157

= 0.0064 + 0.0003

= 0.0067

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See previous:

Photoneutrons

See above:

Delayed Neutrons

See next:

Energy Spectra