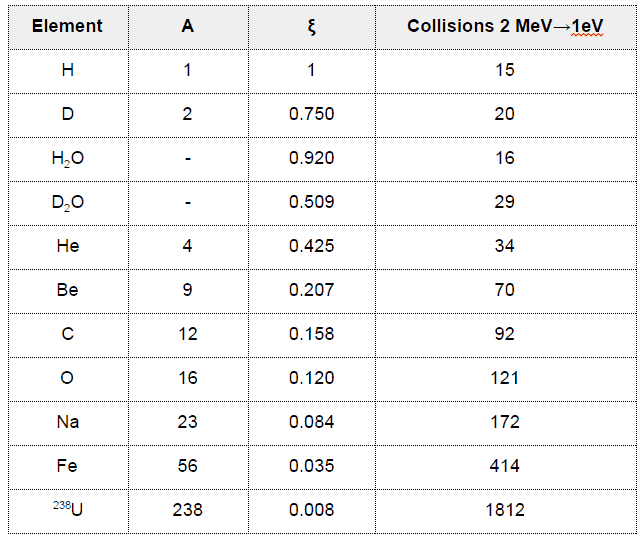
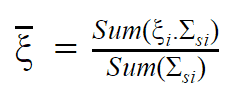Elastic Scattering and Neutron Moderators
To be an effective moderator, the probability of elastic reaction between neutron and the nucleus must be high. In terms of cross-sections, the elastic scattering cross-section of a moderator’s nucleus must be high. Therefore, a high elastic scattering cross-section is important but does not describe the comprehensive capabilities of moderators. To describe the capabilities of a material to slow down neutrons, three new material variables must be defined:
- high cross-section for neutron scattering
- high energy loss per collision
- low cross-section for absorption
- high melting and boiling point
- high thermal conductivity
- high specific heat capacity
- low viscosity
- low activity
- low corrosive
- cheap
Average Logarithmic Energy Decrement
During the scattering reaction, a fraction of the neutron’s kinetic energy is transferred to the nucleus. Using the laws of conservation of momentum and energy and the analogy of collisions of billiard balls for elastic scattering, it is possible to derive the following equation for the mass of target or moderator nucleus (M), the energy of incident neutron (Ei), and the energy of scattered neutron (Es).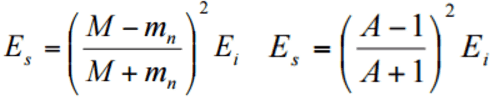 where A is the atomic mass number, in case of the hydrogen (A = 1) as the target nucleus, the incident neutron can be completely stopped. But this works when the direction of the neutron is completely reversed (i.e., scattered at 180°). In reality, the direction of scattering ranges from 0 to 180 °, and the energy transferred also ranges from 0% to maximum. Therefore, the average energy of the scattered neutron is taken as the average of energies with scattering angles 0 and 180°. Moreover, it is useful to work with logarithmic quantities. Therefore one defines the logarithmic energy decrement per collision (ξ) as a key material constant describing energy transfers during a neutron slowing down. ξ is not dependent on energy, only on A and is defined as follows:
where A is the atomic mass number, in case of the hydrogen (A = 1) as the target nucleus, the incident neutron can be completely stopped. But this works when the direction of the neutron is completely reversed (i.e., scattered at 180°). In reality, the direction of scattering ranges from 0 to 180 °, and the energy transferred also ranges from 0% to maximum. Therefore, the average energy of the scattered neutron is taken as the average of energies with scattering angles 0 and 180°. Moreover, it is useful to work with logarithmic quantities. Therefore one defines the logarithmic energy decrement per collision (ξ) as a key material constant describing energy transfers during a neutron slowing down. ξ is not dependent on energy, only on A and is defined as follows: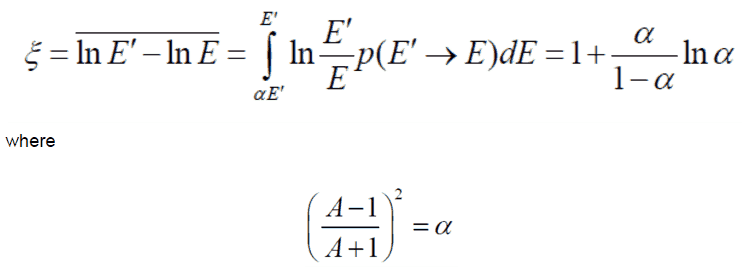 For heavy target nuclei, ξ may be approximated by the following formula:
For heavy target nuclei, ξ may be approximated by the following formula: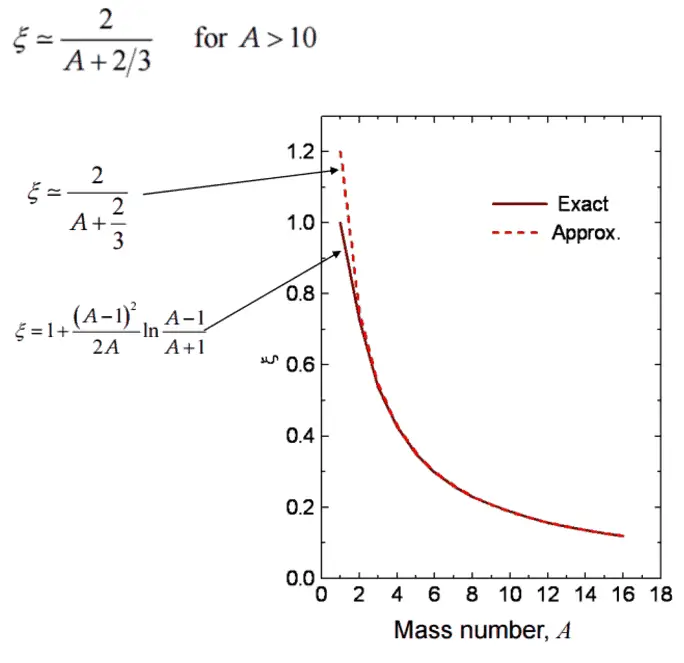 From these equations, it is easy to determine the number of collisions required to slow down a neutron from, for example from 2 MeV to 1 eV.
From these equations, it is easy to determine the number of collisions required to slow down a neutron from, for example from 2 MeV to 1 eV.
Example: Determine the number of collisions required for thermalization for the 2 MeV neutron in the carbon.
ξCARBON = 0.158N(2MeV → 1eV) = ln 2⋅106/ξ =14.5/0.158 = 92