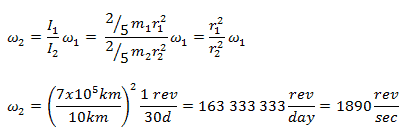In physics, the linear momentum, p = mv, has a rotational analog. It is called angular momentum (rarely, the moment of momentum or rotational momentum), L. For an object rotating about a fixed axis with angular velocity ω, it is defined as:
L = Iω
It is an important quantity in physics because it is a conserved quantity:
The angular momentum of an isolated system remains constant in both magnitude and direction.
When there is zero net torque acting on an object, and the object is rotating about a fixed axis or an axis through its center of mass whose direction doesn’t change, we can write:
I1ω1 = I2ω2 = constant
Like conservation of energy and linear momentum, this principle is a universal conservation law, valid at all scales, from atomic and nuclear systems to the motions of galaxies. The angular momentum is a vector quantity, and therefore it can be generalized as:
The vector sum of the angular momenta of the parts of an isolated system is constant.
This puts a strong constraint on the types of rotational motions which can occur in an isolated system. Suppose one part of the system is given an angular momentum in a given direction. In that case, some other parts must simultaneously be given the same angular momentum in the opposite direction.
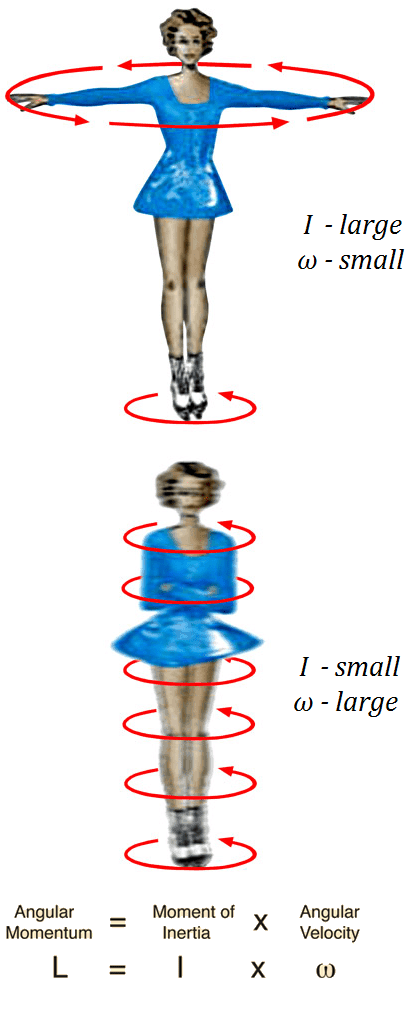
The law of conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs closer to the vertical axis of rotation. By bringing part of the mass of her body closer to the axis, she decreases her body’s moment of inertia. Because angular momentum is the product of moment of inertia (I) and angular velocity (ω), and the angular momentum remains constant according to this law, the angular velocity of the skater must increase.
I1ω1 = I2ω2
Example: Neutron Star Rotation
A neutron star is the collapsed core of a large star (usually of a red giant). Neutron stars are the smallest and densest stars known to exist, but they are rotating extremely rapidly. This rapid rotation is a direct consequence of the law of conservation of angular momentum. As the star’s core collapses, its rotation rate must increase because of the conservation of angular momentum. Hence newly formed neutron stars must rotate up to several hundred times per second. Some neutron stars emit beams of electromagnetic radiation that make them detectable as pulsars.
For example:
Assume a neutron star of a radius of 7 x 105 km, which collapses under its own gravitation to a radius of 10 km. This star rotates at a frequency of 1.0 revolutions every 30 days. Assume that the star is a homogenous sphere at all times and loses no mass.
From the law of conservation of angular momentum:
I1ω1 = I2ω2
where subscripts 1 and 2 refer to the initial star and neutron star, respectively. The moment of inertia of a sphere about its central axis is:
I = ⅖ m1r12
therefore
Conservation of Angular Momentum in Fluid Mechanics
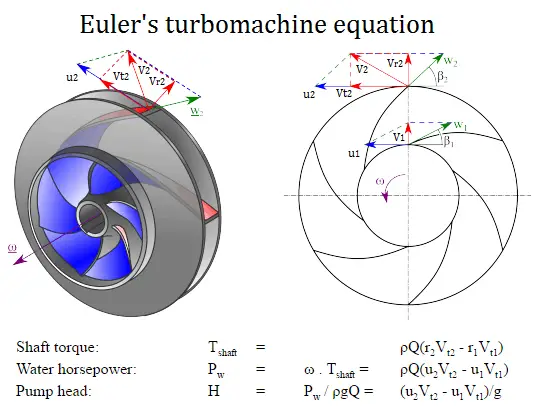
Euler’s turbomachine equation, or sometimes called Euler’s pump equation, plays a central role in turbomachinery as it connects the specific work Y and the geometry and velocities in the impeller. The equation is based on the concepts of conservation of angular momentum and conservation of energy.
Euler’s turbomachine equations are:
Shaft torque: Tshaft = ρQ(r2Vt2 – r1Vt1)
Water horsepower: Pw = ω . Tshaft = ρQ(u2Vt2 – u1Vt1)
Pump head: H = Pw / ρgQ = (u2Vt2 – u1Vt1)/g
where
- r1 and r2 are the diameters of the impeller at the inlet and outlet, respectively.
- u1 and u2 are the absolute velocities of the impeller (u1 = r1 . ω) at the inlet and outlet, respectively.
- Vt1 and Vt2 are the tangential velocities of the flow at the inlet and outlet, respectively.
Euler’s turbomachine equations can predict the impact of changing the impeller geometry on the head. It does not matter when we deal with a pump or with a turbine. If torque and angular velocity are like a sign, work is being done on the fluid (a pump or compressor). If torque and angular velocity are of opposite sign, work is being extracted from the fluid (a turbine). Thus for the design aspect of turbines and pumps, the Euler equations are extremely useful.
