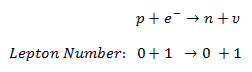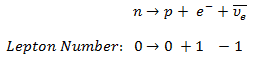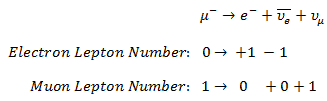In particle physics, the lepton number denotes which particles are leptons and which particles are not. Each lepton has a lepton number of 1, and each antilepton has a lepton number of -1. Other non-leptonic particles have a lepton number of 0. The lepton number is a conserved quantum number in all particle reactions. A slight asymmetry in the laws of physics allowed leptons to be created in the Big Bang.
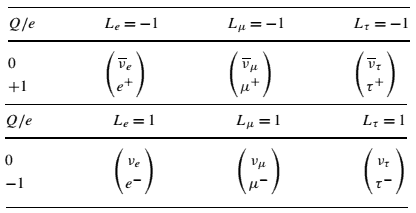 The conservation of lepton number means that whenever a lepton of a certain generation is created or destroyed in a reaction, a corresponding antilepton from the same generation must be created or destroyed. It must be added, and there is a separate requirement for each of the three generations of leptons, the electron, muon, and tau, and their associated neutrinos.
The conservation of lepton number means that whenever a lepton of a certain generation is created or destroyed in a reaction, a corresponding antilepton from the same generation must be created or destroyed. It must be added, and there is a separate requirement for each of the three generations of leptons, the electron, muon, and tau, and their associated neutrinos.
What are Leptons
A lepton is an elementary, half-integer spin (spin 1⁄2) particle that does not undergo strong interactions. Particles that do participate in strong interactions are called hadrons.
There are six leptons in the present structure, the electron, muon, and tau particles and their associated neutrinos. Leptons are said to be elementary particles; they do not appear to be smaller units of matter. They behave as point-like particles. All leptons are fermions, i.e., leptons are spin- 1⁄2 particles, and thus that they are subject to the Pauli exclusion principle. This fact has key implications for the building up of the periodic table of elements.
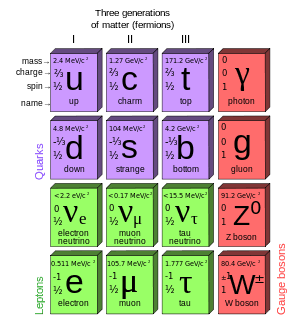
Any of the six elementary particles that (with their antiparticles) are not quarks are leptons. Two main classes of leptons exist:
- Charged leptons. Charged leptons can combine with other particles to form various composite particles such as atoms and positronium.
- Electron. The electron is a negatively charged particle with a mass that is approximately 1/1836 that of the proton. Electrons are located in an electron cloud, which is the area surrounding the nucleus of the atom. The electron is only one member of a class of elementary particles, which forms an atom.
- Muon. The muon is an elementary particle similar to the electron, with an electric charge of −1 e and a spin of ½. Muons are heavier, having more than 200 times as much mass as electrons. The muon is an unstable subatomic particle with a mean lifetime of 2.2 µs.
- Tau. The tau (τ), also called the tau lepton, tau particle, or tauon, is an elementary particle similar to the electron, with an electric charge of −1 e and a spin of ½. Taus is approximately 3,700 times more massive than electrons. Tau leptons have a lifetime of 2.9×10−13 s.
- Neutral leptons (better known as neutrinos) are electrically neutral particles that rarely interact with anything and are consequently rarely observed. A neutrino is an elementary subatomic particle with infinitesimal mass (less than 0.3 eV..?) and no electric charge. Neutrinos are weakly interacting subatomic particles with ½ units of spin.
- Electron neutrino. The electron neutrino is a subatomic lepton elementary particle that has the symbol νe. It has no net electric charge and a spin of ½. Together with the electron, it forms the first generation of leptons, hence the name electron neutrino.
- Muon neutrino. The muon neutrino is a subatomic lepton elementary particle that has the symbol νμ. It has no net electric charge and a spin of ½. Together with the muon, it forms the second generation of leptons, hence the name muon neutrino.
- Tau neutrino. The tau neutrino is a subatomic lepton elementary particle which has the symbol ντ. It has no net electric charge and a spin of ½. Together with the tauon, it forms the third generation of leptons, hence the name tau neutrino.
Conservation of Lepton Number – Electron Capture
Consider the electron capture mode. The reaction involves only first-generation leptons: electrons and neutrinos:
The antineutrino cannot be emitted, because in this case, the conservation law would not be fulfilled. The particle emitted with the neutron must be a neutrino.
Conservation of Lepton Number – Neutron Decay
Consider the decay of the neutron. The reaction involves only first-generation leptons: electrons and neutrinos:
Since the lepton number must be equal to zero on both sides and it was found that the reaction is a three-particle decay (the electrons emitted in beta decay have a continuous rather than a discrete spectrum), the third particle must be an electron antineutrino.
Conservation of Lepton Number – Muon Decay
The observation of the following decay reaction leads to the conclusion that there is a separate lepton number for muons which must also be conserved.
This is, in fact, the most common decay mode of the –.