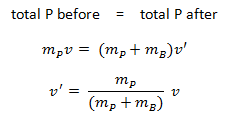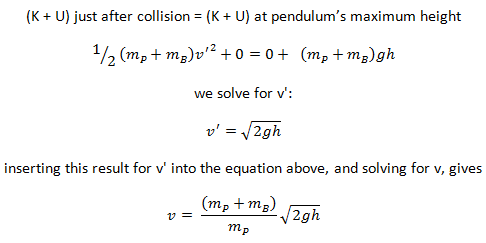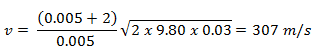Facebook Instagram Youtube Twitter

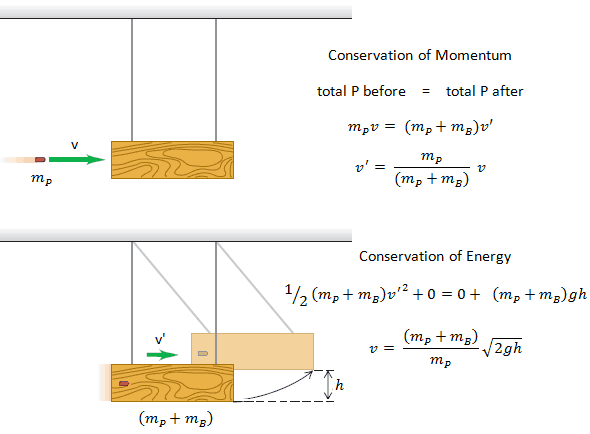
Ballistic Pendulum – Inelastic Collision

Ballistic Pendulum

Ballistic Pendulum
The ballistic pendulum is a kind of “transformer,” exchanging the high speed of a light object (the bullet) for the low speed of a massive object.

A ballistic pendulum is a device for measuring the velocity of a projectile, such as a bullet. The ballistic pendulum is a kind of “transformer,” exchanging the high speed of a light object (the bullet) for the low speed of a massive object (the block). When a bullet is fired into the block, its momentum is transferred to the block. The bullet’s momentum can be determined from the amplitude of the pendulum swing.

When the bullet is embedding itself in the block, it occurs so quickly that the block does not move appreciably. The supporting strings remain nearly vertical, so negligible external horizontal force acts on the bullet–block system, and the horizontal component of momentum is conserved. However, mechanical energy is not conserved during this stage because a nonconservative force does work (the force of friction between bullet and block).

In the second stage, the bullet and block move together. The only forces acting on this system are gravity (a conservative force) and string tensions (which do not work). Thus, as the block swings, mechanical energy is conserved. Momentum is not conserved during this stage because there is a net external force (the forces of gravity and string tension don’t cancel when the strings are inclined).

Equations governing the ballistic pendulum

In the first stage, momentum is conserved, and therefore:

conservation-of-momentum-inelastic

where v is the initial velocity of the projectile of mass mP. v’ is the velocity of the block and embedded projectile (both of mass mP + mB) just after the collision, before they have moved significantly.

In the second stage, mechanical energy is conserved. We choose y = 0 when the pendulum hangs vertically and then y = h when the block and embedded projectile system reach maximum height. The system swings up and comes to rest for an instant at a height y, where its kinetic energy is zero, and the potential energy is (mP + mB)gh. Thus we write the law of conservation of energy:

solution-inelastic-collision

which is the initial velocity of the projectile and our final result.

When we use some realistic numbers:

  • mP = 5 g
  • mB = 2 kg
  • h = 3 cm
  • v = ?

then we have:

solution-example

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Conservation of Energy