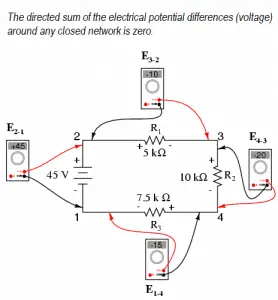
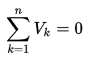 Kirchhoff’s voltage law (KVL)
Kirchhoff’s voltage law (KVL)
The law of conservation of energy can also be used in the analysis of electrical circuits. In the analysis of electrical circuits, the principle of energy conservation provides the basis for the law, known as Kirchhoff’s voltage law (or Kirchhoff’s second law), after German physicist Gustav Robert Kirchhoff.
Kirchhoff’s voltage law states:
The algebraic sum of the voltages (drops or rises) encountered in traversing any circuit loop in a specified direction must be zero.
The algebraic sum of the voltages (drops or rises) encountered in traversing any circuit loop in a specified direction must be zero.
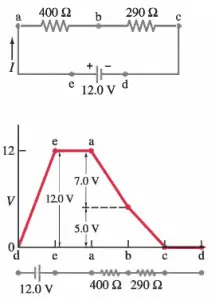 The voltage changes around any closed loop must sum to zero. The sum of the voltage rises is equal to the sum of the voltage drops in a loop. No matter what path you take through an electric circuit, if you return to your starting point, you must measure the same voltage, constraining the net change around the loop to be zero.
The voltage changes around any closed loop must sum to zero. The sum of the voltage rises is equal to the sum of the voltage drops in a loop. No matter what path you take through an electric circuit, if you return to your starting point, you must measure the same voltage, constraining the net change around the loop to be zero.
Since voltage is electric potential energy per unit charge, the voltage law can be seen to be a consequence of the conservation of energy. This rule is equivalent to saying that each point on a mountain has only one elevation above sea level. If you start from any point and return to it after walking around the mountain, the algebraic sum of the elevation changes that you encounter must be zero.
The voltage law has great practical utility in the analysis of electric circuits. It is used in conjunction with the current law in many circuit analysis tasks.