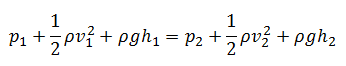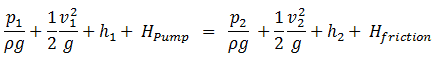The law of conservation of energy can also be used in the analysis of flowing fluids.
Bernoulli’s equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. The general energy equation is simplified to:
This equation is the most famous in fluid dynamics. Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive but seems less so when you consider the pressure to be energy density. In the high-velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume. The equation above assumes that no non-conservative forces (e.g.,, friction forces) act on the fluid. This is a very strong assumption.
Extended Bernoulli’s equation
Bernoulli’s equation can be modified to take into account gains and losses of the head caused by external forces and non-conservative forces. The resulting equation referred to as the extended Bernoulli’s equation is useful in solving most fluid flow problems. The following equation is one form of the extended Bernoulli equation.
where:
- h = height above reference level (m)
- v = average velocity of fluid (m/s)
- p = pressure of fluid (Pa)
- Hpump = head added by pump (m)
- Hfriction = head loss due to fluid friction (m)
- g = acceleration due to gravity (m/s2)
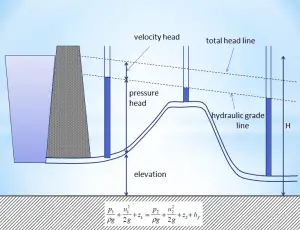
The head loss (or the pressure loss) due to fluid friction (Hfriction) represents the energy used in overcoming friction caused by the pipe walls. The head loss that occurs in pipes is dependent on the flow velocity, pipe diameter, and length, and a friction factor based on the roughness of the pipe and the Reynolds number of the flow. A piping system containing many pipe fittings and joints, tube convergence, divergence, turns, surface roughness, and other physical properties will also increase the head loss of a hydraulic system.
Although the head loss represents a loss of energy, it does not represent a loss of total energy of the fluid. The total energy of the fluid is conserved as a consequence of the law of conservation of energy. In reality, the head loss due to friction results in an equivalent increase in the fluid’s internal energy (temperature increases).
This phenomenon can also be seen in the case of reactor coolant pumps. Generally, reactor coolant pumps are very powerful, they can consume up to 6 MW each, and therefore they can be used for heating the primary coolant before a reactor startup, for example, from 30°C at cold zero power (CZP) to 290°C at hot zero power (HZP).