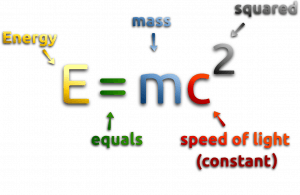At the beginning of the 20th century, the notion of mass underwent a radical revision. The mass lost its absoluteness. One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula E = mc2. In other words, energy equals mass multiplied by the speed of light squared. Because the speed of light is very large, the formula implies that any small amount of matter contains a very large amount of energy. The mass of an object was seen as equivalent to energy, interconvertible with energy, and increasing significantly at exceedingly high speeds near that of light. The total energy was understood to comprise its rest mass and its increase of mass caused by an increase in kinetic energy.
In the special theory of relativity, certain types of matter may be created or destroyed. Still, the mass and energy associated with such matter remain unchanged in quantity in all of these processes. It was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons, and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E = mc2), this binding energy is proportional to this mass difference, known as the mass defect.
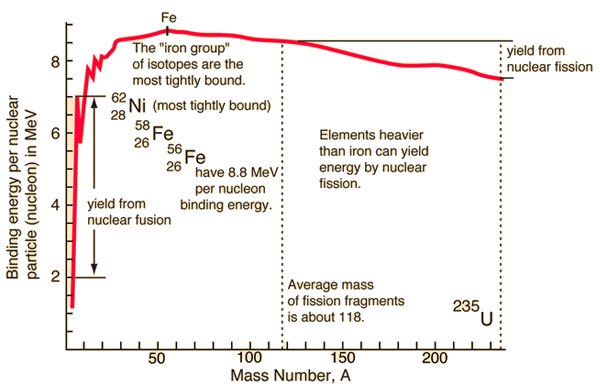
Source: hyperphysics.phy-astr.gsu.edu
During the nuclear splitting or nuclear fusion, some of the mass of the nucleus gets converted into huge amounts of energy. Thus this mass is removed from the total mass of the original particles, and the mass is missing in the resulting nucleus. The nuclear binding energies are enormous, and they are a million times greater than the electron binding energies of atoms.
Generally, in both chemical and nuclear reactions, some conversion between rest mass and energy occurs so that the products generally have smaller or greater mass than the reactants. Therefore the new conservation principle is the conservation of mass energy.
See also: Energy Release from Fission.
Example: Mass-energy defect of a 63Cu
Calculate the mass defect of a 63Cu nucleus if the actual mass of 63Cu in its nuclear ground state is 62.91367 u.
63Cu nucleus has 29 protons and also has (63 – 29) 34 neutrons.
The mass of a proton is 1.00728 u, and a neutron is 1.00867 u.
The combined mass is: 29 protons x (1.00728 u/proton) + 34 neutrons x (1.00867 u/neutron) = 63.50590 u
The mass defect is Δm = 63.50590 u – 62.91367 u = 0.59223 u
Convert the mass defect into energy (nuclear binding energy).
(0.59223 u/nucleus) x (1.6606 x 10-27 kg/u) = 9.8346 x 10-28 kg/nucleus
ΔE = (9.8346 x 10-28 kg/nucleus) x (2.9979 x 108 m/s)2 = 8.8387 x 10-11 J/nucleus
The energy calculated in the previous example is nuclear binding energy. However, the nuclear binding energy may be expressed as kJ/mol (for better understanding).
Calculate the nuclear binding energy of 1 mole of 63Cu:
(8.8387 x 10-11 J/nucleus) x (1 kJ/1000 J) x (6.022 x 1023 nuclei/mol) = 5.3227 x 1010 kJ/mol of nuclei.
One mole of 63Cu (~63 grams) is bound by the nuclear binding energy (5.3227 x 1010 kJ/mol), which is equivalent to:
- 14.8 million kilowatt-hours (≈ 15 GW·h)
- 336,100 US gallons of automotive gasoline
Example: Mass defect of the reactor core
Calculate the mass defect of the 3000MWth reactor core after one year of operation.
It is known the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of antineutrinos that are radiated away.
The reaction rate per entire 3000MWth reactor core is about 9.33×1019 fissions/second.
The overall energy release in the units of joules is:
200×106 (eV) x 1.602×10-19 (J/eV) x 9.33×1019 (s-1) x 31.5×106 (seconds in year) = 9.4×1016 J/year
The mass defect is calculated as:
Δm = ΔE/c2
Δm = 9.4×1016 / (2.9979 x 108)2 = 1.046 kg
That means in a typical 3000MWth reactor core, about 1 kilogram of the matter is converted into pure energy.
Note that a typical annual uranium load for a 3000MWth reactor core is about 20 tons of enriched uranium (i.e., about 22.7 tons of UO2). The entire reactor core may contain about 80 tonnes of enriched uranium.
Mass defect directly from E=mc2
The mass defect can be calculated directly from the Einstein relationship (E = mc2) as:
Δm = ΔE/c2
Δm = 3000×106 (W = J/s) x 31.5×106 (seconds in year) / (2.9979 x 108)2 = 1.051 kg