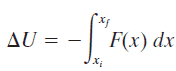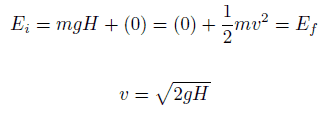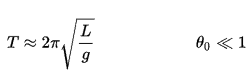First, the principle of the Conservation of Mechanical Energy was stated:
The total mechanical energy (defined as the sum of its potential and kinetic energies) of a particle being acted on by only conservative forces is constant.
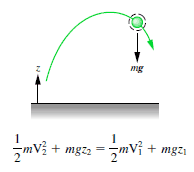 An isolated system is one in which no external force causes energy changes. If only conservative forces act on an object and U is the potential energy function for the total conservative force, then:
An isolated system is one in which no external force causes energy changes. If only conservative forces act on an object and U is the potential energy function for the total conservative force, then:
Emech = U + K
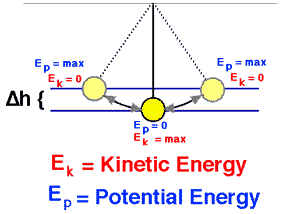
The potential energy, U, depends on the position of an object subjected to a conservative force.
It is defined as the object’s ability to do work and is increased as the object is moved in the opposite direction of the direction of the force.
The potential energy associated with a system consisting of Earth and a nearby particle is gravitational potential energy.
The kinetic energy, K, depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them.
K = ½ mv2
The definition mentioned above (Emech = U + K) assumes that the system is free of friction and other non-conservative forces. The difference between a conservative and a non-conservative force is that when a conservative force moves an object from one point to another, the work done by the conservative force is independent of the path.
In any real situation, frictional forces and other non-conservative forces are present. Still, their effects on the system are so small that the principle of conservation of mechanical energy can be used as a fair approximation in many cases. For example, the frictional force is a non-conservative force because it reduces the mechanical energy in a system.
Note that non-conservative forces do not always reduce mechanical energy. A non-conservative force changes the mechanical energy. Some forces increase the total mechanical energy, like the force provided by a motor or engine, which is also a non-conservative force.
The Law of Conservation of Energy – Non-conservative Forces
We now take into account non-conservative forces such as friction since they are important in real situations. For example, consider the pendulum again, but this time let us include air resistance. The pendulum will slow down because of friction. In this and other natural processes, the mechanical energy (sum of the kinetic and potential energies) does not remain constant but decreases. Because frictional forces reduce the mechanical energy (but not the total energy), they are called non-conservative forces (or dissipative forces). But in the nineteenth century, it was demonstrated the total energy is conserved in any process. In the case of the pendulum, its initial kinetic energy is all transformed into thermal energy.
For each type of force, conservative or non-conservative, it has always been found possible to define a type of energy that corresponds to the work done by such a force. And it has been found experimentally that the total energy E always remains constant. The general law of conservation of energy can be stated as follows:
The total energy E of a system (the sum of its mechanical energy and its internal energies, including thermal energy) can change only by amounts of energy transferred to or from the system.