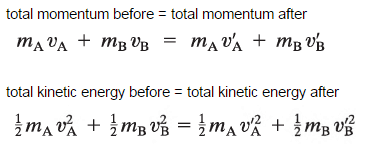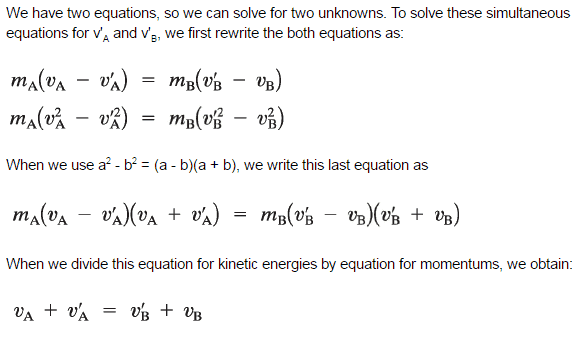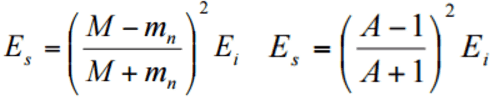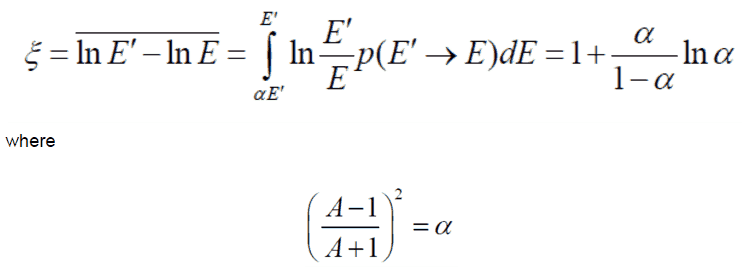A perfectly elastic collision is defined as one in which there is no net conversion of kinetic energy into other forms (such as heat or noise). For the brief moment during which the two objects are in contact, some (or all) of the energy is stored momentarily in the form of elastic potential energy. But if we compare the total kinetic energy just before the collision with the total kinetic energy just after the collision, they are found to be the same. We say that the total kinetic energy is conserved.
- Large-scale interactions between satellites and planets are perfectly elastic, like the slingshot type gravitational interactions (also known as a planetary swing-by or a gravity-assist maneuver).
- Collisions between very hard spheres may be nearly elastic, so it is useful to calculate the limiting case of an elastic collision.
- Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles deflect by the electromagnetic force.
- Rutherford scattering is the elastic scattering of charged particles also by the electromagnetic force.
- A neutron-nucleus scattering reaction may also be elastic, but in this case, the neutron is deflected by a strong nuclear force.