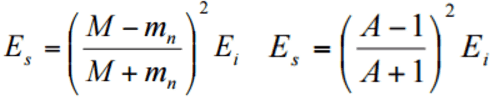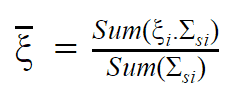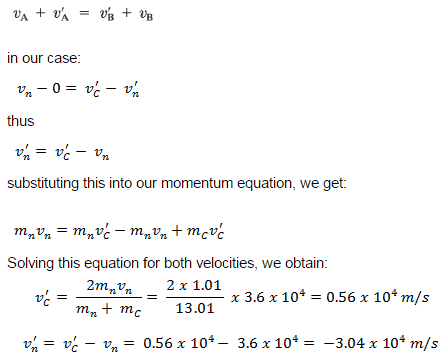Elastic Collisions
A perfectly elastic collision is defined as one in which there is no net conversion of kinetic energy into other forms (such as heat or noise). For the brief moment during which the two objects are in contact, some (or all) of the energy is stored momentarily in the form of elastic potential energy. But if we compare the total kinetic energy just before the collision with the total kinetic energy just after the collision, and they are found to be the same, then we say that the total kinetic energy is conserved.
Elastic Nuclear Collision
See also: Neutron Moderators
It is known the fission neutrons are of importance in any chain-reacting system. All neutrons produced by fission are born as fast neutrons with high kinetic energy. Before such neutrons can efficiently cause additional fissions, they must be slowed down by collisions with nuclei in the reactor’s moderator. The probability of the fission U-235 becomes very large at the thermal energies of slow neutrons. This fact implies an increase in the multiplication factor of the reactor (i.e., lower fuel enrichment is needed to sustain a chain reaction).
The neutrons released during fission with an average energy of 2 MeV in a reactor on average undergo many collisions (elastic or inelastic) before they are absorbed. During the scattering reaction, a fraction of the neutron’s kinetic energy is transferred to the nucleus. It is possible to derive the following equation for the mass of target or moderator nucleus (M), the energy of incident neutron (Ei), and the energy of scattered neutron (Es) using the laws of conservation of momentum and energy and the analogy of collisions of billiard balls for elastic scattering.
where A is the atomic mass number, in case of the hydrogen (A = 1) as the target nucleus, the incident neutron can be completely stopped. But this works when the direction of the neutron is completely reversed (i.e., scattered at 180°). In reality, the direction of scattering ranges from 0 to 180 °, and the energy transferred also ranges from 0% to maximum. Therefore, the average energy of the scattered neutron is taken as the average of energies with scattering angles 0 and 180°.
Moreover, it is useful to work with logarithmic quantities. Therefore one defines the logarithmic energy decrement per collision (ξ) as a key material constant describing energy transfers during a neutron slowing down. ξ is not dependent on energy, only on A and is defined as follows: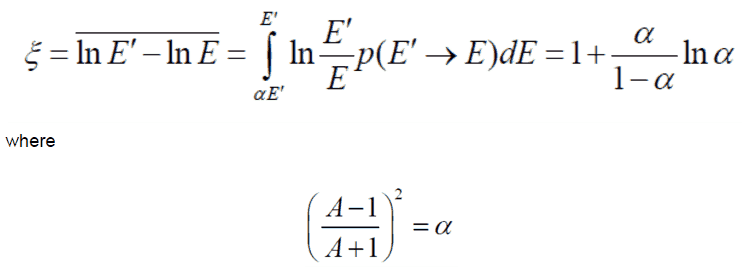
For heavy target nuclei, ξ may be approximated by the following formula:
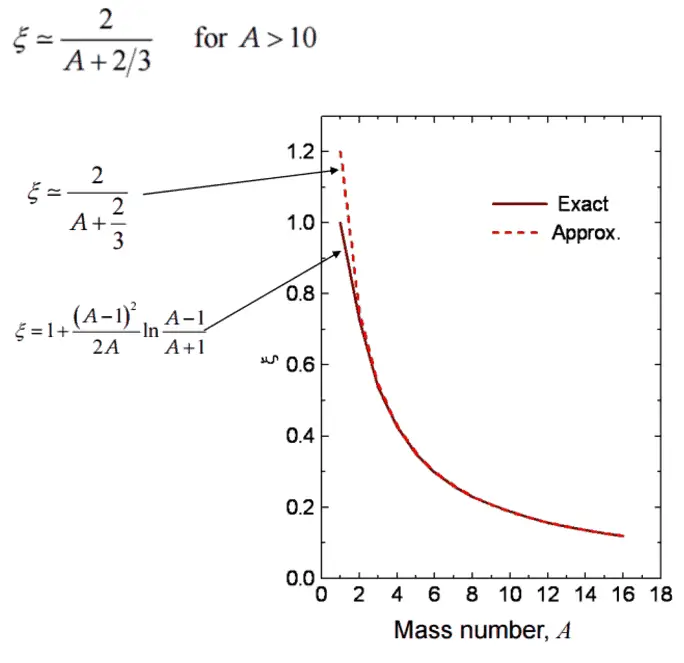From these equations, it is easy to determine the number of collisions required to slow down a neutron from, for example from 2 MeV to 1 eV.
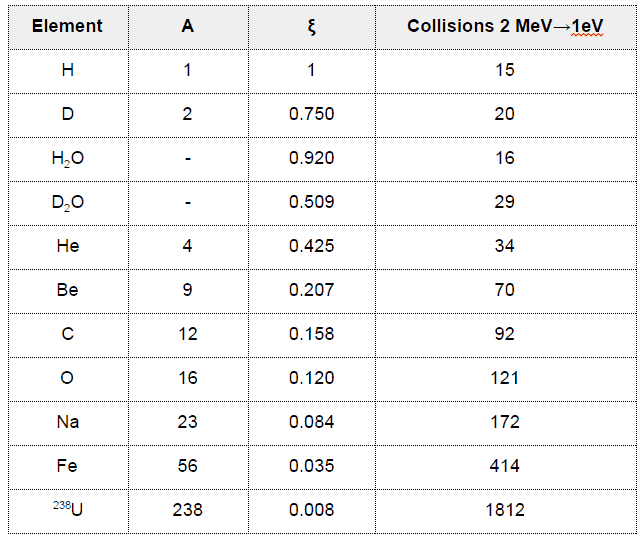
Example: Determine the number of collisions required for thermalization for the 2 MeV neutrons in the carbon.
ξCARBON = 0.158
N(2MeV → 1eV) = ln 2⋅106/ξ =14.5/0.158 = 92
For a mixture of isotopes:
Example: Elastic Nuclear Collision
A neutron (n) of mass 1.01 u traveling with a speed of 3.60 x 104m/s interacts with a carbon (C) nucleus (mC = 12.00 u) initially at rest in an elastic head-on collision.
What are the velocities of the neutron and carbon nucleus after the collision?
Solution:
This is an elastic head-on collision of two objects with unequal masses. We have to use the conservation laws of momentum and kinetic energy and apply them to our system of two particles.
We can solve this system of equations or use the equation derived in the previous section. This equation stated that the relative speed of the two objects after the collision has the same magnitude (but opposite direction) as before the collision, no matter what the masses are.
The minus sign for v’ tells us that the neutron scatters back of the carbon nucleus because the carbon nucleus is significantly heavier. On the other hand, its speed is less than its initial speed. This process is known as neutron moderation, and it significantly depends on the mass of moderator nuclei.
