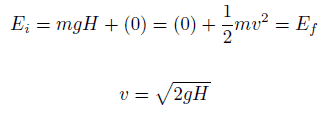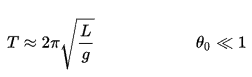Facebook Instagram Youtube Twitter

Example of Conservation of Mechanical Energy – Pendulum

conservartion-of-mechanical-energy-pendulumAssume a pendulum (ball of mass m suspended on a string of length L that we have pulled up so that the ball is a height H < L above its lowest point on the arc of its stretched string motion. The pendulum is subjected to the conservative gravitational force where frictional forces like air drag and friction at the pivot are negligible.

We release it from rest. How fast is it going at the bottom?

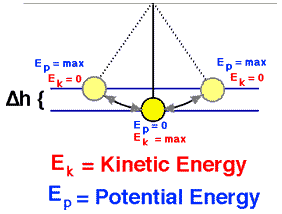
conservartion-of-mechanical-energy-pendulum2

The pendulum reaches the greatest kinetic energy and least potential energy when in the vertical position because it will have the greatest speed and be nearest the Earth at this point. On the other hand, it will have its least kinetic energy and greatest potential energy at the extreme positions of its swing because it has zero speed and is farthest from Earth at these points.

If the amplitude is limited to small swings, the period T of a simple pendulum, the time is taken for a complete cycle, is:

period-of-pendulum-conservation-of-energy

where L is the length of the pendulum and g is the local acceleration of gravity. For small swings, the period of swing is approximately the same for different size swings. That is, the period is independent of amplitude.

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Conservation of Energy