In thermodynamics, the concept of energy is broadened to account for other observed changes. The principle of conservation of energy is extended to include a wide variety of ways systems interact with their surroundings. The only ways the energy of a closed system can be changed are through the transfer of energy by work or by heat. Further, based on the experiments of Joule and others, a fundamental aspect of the energy concept is that energy is conserved. This principle is known as the first law of thermodynamics. The first law of thermodynamics can be written in various forms:
In words:
Equation form:
∆Eint = Q – W
where Eint represents the internal energy of the material, which depends only on the material’s state (temperature, pressure, and volume), Q is the net heat added to the system, and W is the net work done by the system. We must be careful and consistent in following the sign conventions for Q and W. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative, and Eint will increase.
Similarly, Q is positive for heat added to the system, so Q is negative if heat leaves the system. This tells us the following: The internal energy of a system tends to increase if heat is absorbed by the system or if positive work is done on the system. Conversely, the internal energy tends to decrease if heat is lost by the system or if negative work is done on the system. It must be added Q and W are path-dependent, while Eint is path-independent.
Differential form:
dEint = dQ – dW
The internal energy Eint of a system tends to increase if energy is added as heat Q and tends to decrease if energy is lost as work W is done by the system.
Open System – Closed System – Isolated System
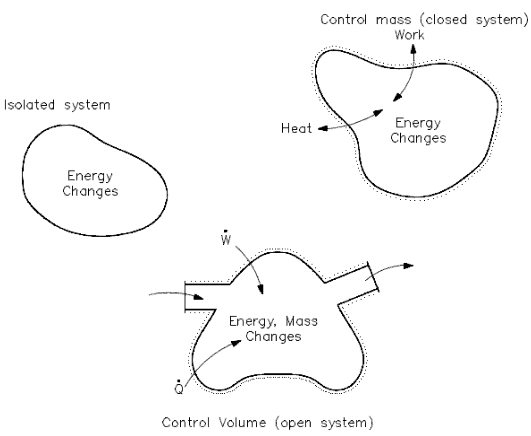 Heat and/or work can be directed into or out of the control volume. But, for convenience and as a standard convention, the net energy exchange is presented here, with the net heat exchange assumed to be into the system and the net work assumed to be out of the system. If no mass crosses the boundary, but work and/or heat do, the system is referred to as a “closed” system. If mass, work, and heat do not cross the boundary (that is, the only energy exchanges taking place are within the system), the system is referred to as an isolated system. Isolated and closed systems are nothing more than specialized cases of the open system.
Heat and/or work can be directed into or out of the control volume. But, for convenience and as a standard convention, the net energy exchange is presented here, with the net heat exchange assumed to be into the system and the net work assumed to be out of the system. If no mass crosses the boundary, but work and/or heat do, the system is referred to as a “closed” system. If mass, work, and heat do not cross the boundary (that is, the only energy exchanges taking place are within the system), the system is referred to as an isolated system. Isolated and closed systems are nothing more than specialized cases of the open system.
