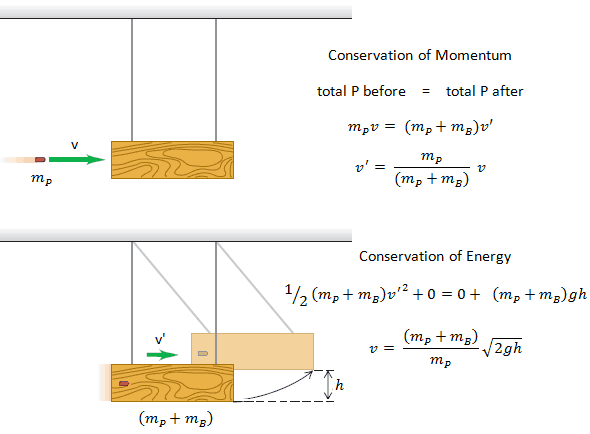
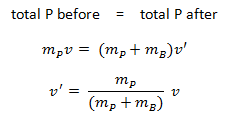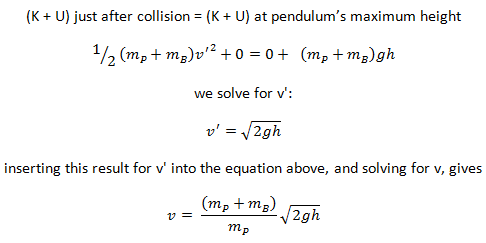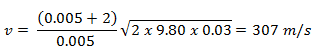An inelastic collision is when part of the kinetic energy is changed to some other form of energy in the collision. Any macroscopic collision between objects will convert some kinetic energy into internal energy and other forms of energy, so no large-scale impacts are perfectly elastic. For example, in collisions of common bodies, such as two cars, some energy is always transferred from kinetic energy to other forms of energy, such as thermal energy or energy of sound. The inelastic collision of two bodies always involves a loss in the kinetic energy of the system. The greatest loss occurs if the bodies stick together, in which case the collision is called a completely inelastic collision. Thus, the system’s kinetic energy is not conserved, while the total energy is conserved as required by the general principle of conservation of energy. Momentum is conserved in inelastic collisions, but one cannot track the kinetic energy through the collision since some of it is converted to other forms of energy.
In nuclear physics, an inelastic collision is when the incoming particle causes the nucleus to strike to become excited or break up. Deep inelastic scattering is a method of probing the structure of subatomic particles in much the same way as Rutherford probed the inside of the atom (see Rutherford scattering).
In nuclear reactors, inelastic collisions are of importance in neutron moderation process. An inelastic scattering plays an important role in slowing down neutrons, especially at high energies and by heavy nuclei. Inelastic scattering occurs above threshold energy. This threshold energy is higher than the energy of the first excited state of the target nucleus (due to the laws of conservation), and it is given by the following formula:
Et = ((A+1)/A)* ε1
where Et is known as the inelastic threshold energy and ε1 is the energy of the first excited state. Therefore especially scattering data of 238U, which is a major component of nuclear fuel in commercial power reactors, are one of the most important data in the neutron transport calculations in the reactor core.