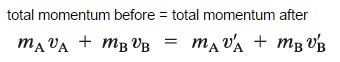What is Conservation of Momentum

law of conservation of energy - pendulum — Newton’s cradle. A device that demonstrates the Law of Conservation of Mechanical Energy and Momentum.

In general, the law of conservation of momentum or principle of momentum conservation states that the momentum of an isolated system is a constant. The vector sum of the momenta (momentum is equal to the mass of an object multiplied by its velocity) of all the objects of a system cannot be changed by interactions within the system. In classical mechanics, this law is implied by Newton’s laws. This principle is a direct consequence of Newton’s third law.

Let us assume the one-dimensional elastic collision of two billiard balls, ball A and ball B. We assume the net external force on this system of two balls is zero—that is, the only significant forces during the collision are the forces that each ball exerts on the other. According to Newton’s third law, the two forces are always equal in magnitude and opposite direction. Hence, the impulses that act on the two balls are equal and opposite, and the changes in momentum of the two balls are equal and opposite.

These two balls are moving with velocities v_A and v_B along the x-axis before the collision. After the collision, their velocities are v’A and v’B. The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum after the collision.

The law of conservation of linear momentum in words:

If no net external force acts on a system of particles, the total linear momentum of the system cannot change.

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Laws of Conservation