Conservation of Energy
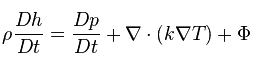 where h is enthalpy, k is the thermal conductivity of the fluid, T is temperature, and Φ is the viscous dissipation function.
where h is enthalpy, k is the thermal conductivity of the fluid, T is temperature, and Φ is the viscous dissipation function.
Bernoulli’s Theorem
 Bernoulli’s theorem can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
Bernoulli’s theorem can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
- steady flow system,
- density is constant (which also means the fluid is incompressible),
- no work is done on or by the fluid,
- no heat is transferred to or from the fluid,
- no change occurs in the internal energy,
- the equation relates the states at two points along a single streamline (not conditions on two different streamlines)
Under these conditions, the general energy equation is simplified to:
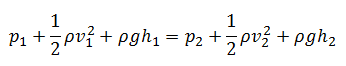
This equation is the most famous in fluid dynamics. Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive but seems less so when you consider the pressure to be energy density. In the high-velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume.