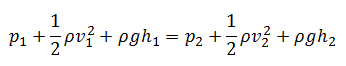Bernoulli’s equation for incompressible fluids can be derived from Euler’s equations of motion under rather severe restrictions.
- The velocity must be derivable from a velocity potential.
- External forces must be conservative. That is, derivable from a potential.
- The density must either be constant or a function of the pressure alone.
- Thermal effects, such as natural convection, are ignored.
The Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow in fluid dynamics. Euler equations can be obtained by linearization of these Navier–Stokes equations.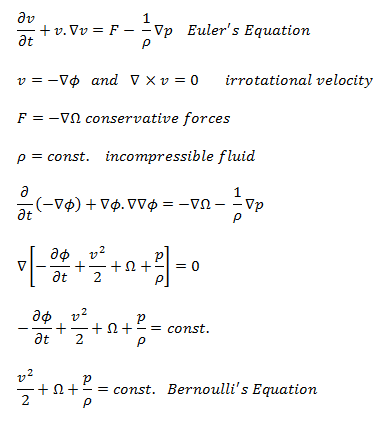
Bernoulli’s Equation
 Bernoulli’s equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
Bernoulli’s equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
- steady flow system,
- density is constant (which also means the fluid is incompressible),
- no work is done on or by the fluid,
- no heat is transferred to or from the fluid,
- no change occurs in the internal energy,
- the equation relates the states at two points along a single streamline (not conditions on two different streamlines)
Under these conditions, the general energy equation is simplified to: