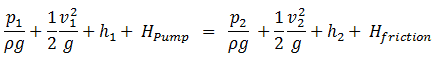Facebook Instagram Youtube Twitter

Extended Bernoulli’s Equation

Two main assumptions were applied to the derivation of the simplified Bernoulli equation.

  • The first restriction on Bernoulli’s equation is that no work is allowed to be done on or by the fluid. This is a significant limitation because most hydraulic systems (especially in nuclear engineering) include pumps. This restriction prevents two points in a fluid stream from being analyzed if a pump exists between the two points.
  • The second restriction on simplified Bernoulli’s equation is that no fluid friction can solve hydraulic problems. In reality, friction plays a crucial role. The total head possessed by the fluid cannot be transferred completely and is lossless from one point to another. In reality, one purpose of pumps incorporated in a hydraulic system is to overcome the losses in pressure due to friction.
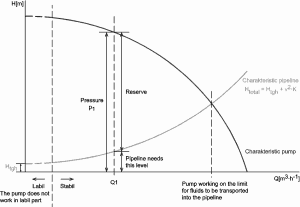
Q-H characteristic diagram of centrifugal pump and of pipeline
Q-H characteristic diagram of centrifugal pump and pipeline

Due to these restrictions, most of the practical applications of the simplified Bernoulli equation to real hydraulic systems are very limited. The simplified Bernoulli equation must be modified to deal with both head losses and pump work.

The Bernoulli equation can be modified to take into account gains and losses of the head. The resulting equation referred to as the extended Bernoulli’s equation is very useful in solving most fluid flow problems. The following equation is one form of the extended Bernoulli equation.

Extended Bernoulli Equation

where:
h = height above reference level (m)
v = average velocity of fluid (m/s)
p = pressure of fluid (Pa)
Hpump = head added by pump (m)
Hfriction = head loss due to fluid friction (m)
g = acceleration due to gravity (m/s2)

The head loss (or the pressure loss) due to fluid friction (Hfriction) represents the energy used in overcoming friction caused by the pipe walls. The head loss that occurs in pipes is dependent on the flow velocity, pipe diameter, and length, and a friction factor based on the roughness of the pipe and the Reynolds number of the flow. A piping system containing many pipe fittings and joints, tube convergence, divergence, turns, surface roughness, and other physical properties will also increase the head loss of a hydraulic system.

Although the head loss represents a loss of energy, it does not represent a loss of total energy of the fluid. The total energy of the fluid is conserved as a consequence of the law of conservation of energy. In reality, the head loss due to friction results in an equivalent increase in the fluid’s internal energy (temperature increases).

Most methods for evaluating head loss due to friction are based almost exclusively on experimental evidence. This will be discussed in following sections.

 
Example: Frictional Head Loss
Water at 20°C is pumped through a smooth 12-cm-diameter pipe 10 km long, at a flow rate of 75 m3/h. The inlet is fed by a pump at an absolute pressure of 2.4 MPa.
The exit is at standard atmospheric pressure (101 kPa) and is 200 m higher.

Calculate the frictional head loss Hf, and compare it to the flow v2/(2g) velocity head.

Solution:

Since the pipe diameter is constant, the average velocity and velocity head is the same everywhere:

vout = Q/A = 75 [m3/h] * 3600 [s/h] / 0.0113 [m2] = 1.84 m/s

Velocity head:

Velocity head = vout2/(2g) = 1.842 / 2*9.81 = 0.173 m

In order to find the frictional head loss, we have to use extended Bernoulli’s equation:

Extended Bernoulli Equation

Head loss:

2 400 000 [Pa] / 1000 [kg/m3] * 9.81 [m/s2]  + 0.173 [m] + 0 [m] = 101 000 [Pa] / 1000 [kg/m3] * 9.81 [m/s2] + 0.173 [m]+ 200 [m] + Hf

Hf  = 244.6 – 10.3 – 200 = 34.3 m

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See above:

Bernoulli’s Principle