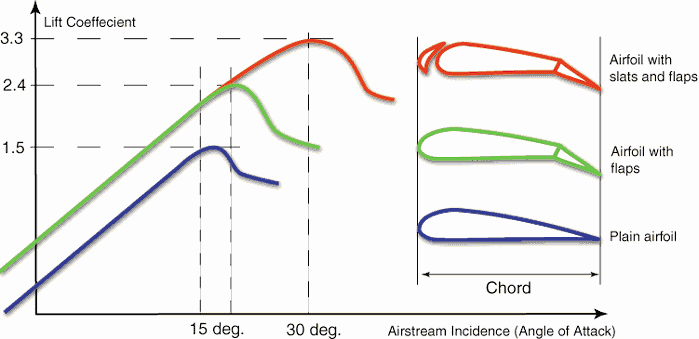
Bernoulli’s Equation
 Bernoulli’s equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
Bernoulli’s equation can be considered a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in the following points:
- steady flow system,
- density is constant (which also means the fluid is incompressible),
- no work is done on or by the fluid,
- no heat is transferred to or from the fluid,
- no change occurs in the internal energy,
- the equation relates the states at two points along a single streamline (not conditions on two different streamlines)
Under these conditions, the general energy equation is simplified to:
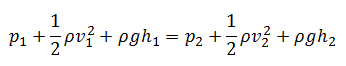
This equation is the most famous equation in fluid dynamics. Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive but seems less so when you consider the pressure to be energy density. In the high-velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume.
Lift Force – Bernoulli’s Principle
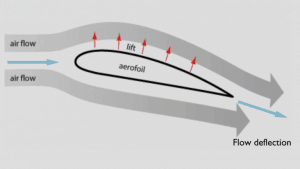
In general, the lift is an upward-acting force on an aircraft wing or airfoil. There are several ways to explain how an airfoil generates lift. Some theories are more complicated or more mathematically rigorous than others. Some theories are incorrect. There are theories based on Bernoulli’s principle, and theories are based directly on Newton’s third law.
The explanation based on Newton’s third law states that the lift is caused by a flow deflection of the airstream behind the airfoil. The airfoil generates a lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the airfoil. This is a very simple explanation.
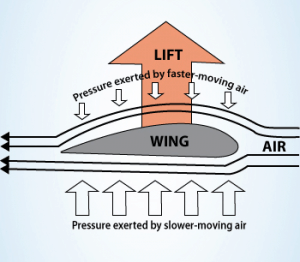
Bernoulli’s principle combined with the continuity equation can also be used to determine the lift force on an airfoil if the behavior of the fluid flow in the vicinity of the foil is known. In this explanation, the shape of an airfoil is crucial. The shape of an airfoil causes air to flow faster on top than on the bottom. According to Bernoulli’s principle, faster-moving air exerts less pressure, and therefore the air must exert an upward force on the airfoil (as a result of a pressure difference).
The use of Bernoulli’s principle may not be correct. Bernoulli’s principle assumes incompressibility of the air, but in reality, the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle. There are two main popular explanations of lift:
- Explanation based on downward deflection of the flow – Newton’s third law
- Explanation based on changes in flow speed and pressure – Continuity principle and Bernoulli’s principle
Both explanations correctly identify some aspects of the lift forces but leave other important aspects of the phenomenon unexplained. A more comprehensive explanation involves both changes in flow speed and downward deflection and requires looking at the flow in more detail.
See more: Doug McLean, Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons Ltd. 2013. ISBN: 978-1119967514