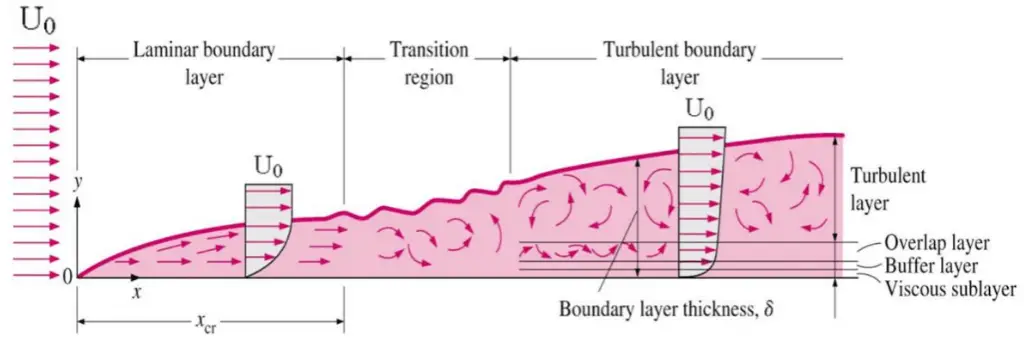
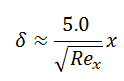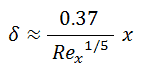We define the thickness of the boundary layer as the distance from the wall to the point where the velocity is 99% of the “free stream” velocity. For laminar boundary layers over a flat plate, the Blasius solution of the flow governing equations gives:
where Rex is the Reynolds number based on the length of the plate.
For a turbulent flow, the boundary layer thickness is given by:
This equation was derived with several assumptions. The turbulent boundary layer thickness formula assumes that the flow is turbulent right from the start of the boundary layer.
Example: Boundary Layer Thickness
Consider a water flow (20°C) at v = 0.1 m/s past a flat plate 1 m long. Compute the boundary layer thickness in the middle of the plate. Assume that the kinematic viscosity of water at 20°C is equal to 1×10-6 m2/s.
The Reynolds number for the middle of the plate is equal to:
ReL/2 = 0.1 [m/s] x 0.5 [m] / 1×10-6 [m2/s] = 50 000
This satisfies the laminar conditions. The boundary layer thickness is therefore equal to:
δ ≈ 5.0 x 0.5 / (50 000)½ = 0.011 m