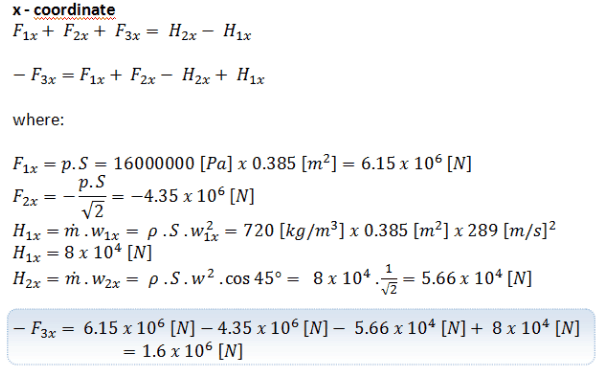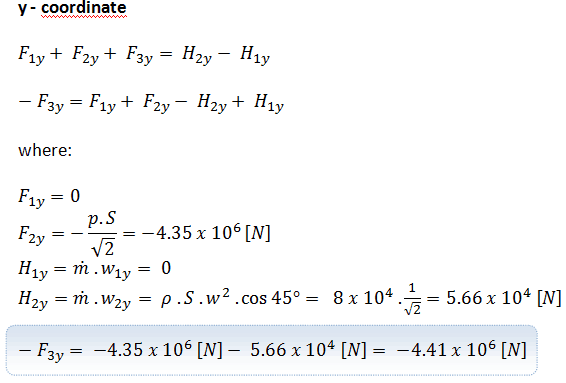In general, the law of conservation of momentum or principle of momentum conservation states that the momentum of an isolated system is a constant. The vector sum of the momenta (momentum is equal to the mass of an object multiplied by its velocity) of all the objects of a system cannot be changed by interactions within the system. In classical mechanics, this law is implied by Newton’s laws.
In fluid dynamics, the analysis of motion is performed in the same way as in solid mechanics – using Newton’s laws of motion. As can be seen, moving fluids are exerting forces. The lift force on an aircraft is exerted by the air moving over the wing.
A jet of water from a hose exerts a force on whatever it hits. But here, it is not clear what mass of moving fluid we should use, and therefore it is necessary to use a different form of the equation.
Newton’s 2nd law can be written:
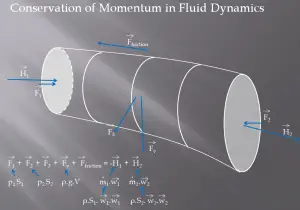 We assume fluid to be both steady and incompressible. To determine the rate of change of momentum for a fluid, we will consider a stream tube (control volume) as we did for the Bernoulli equation. In this control volume, any change in momentum of the fluid within a control volume is due to the action of external forces on the fluid within the volume.
We assume fluid to be both steady and incompressible. To determine the rate of change of momentum for a fluid, we will consider a stream tube (control volume) as we did for the Bernoulli equation. In this control volume, any change in momentum of the fluid within a control volume is due to the action of external forces on the fluid within the volume.
As can be seen from the picture, the control volume method can analyze the law of conservation of momentum in a fluid. A control volume is an imaginary surface enclosing a volume of interest. The control volume can be fixed or moving, and it can be rigid or deformable. To determine all forces acting on the surfaces of the control volume, we have to solve the conservation laws in this control volume.
The first conservation equation we have to consider in the control volume is the continuity equation (the law of conservation of matter). In the simplest form, it is represented by the following equation:
∑ṁin = ∑ṁout
Sum of mass flow rates entering per unit time = Sum of mass flow rates leaving per unit time
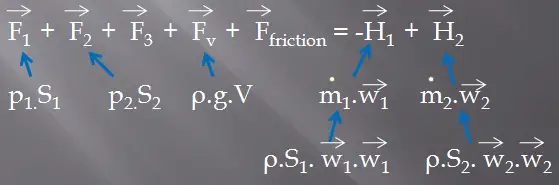
The second conservation equation we have to consider in the control volume is the momentum formula.
Momentum Formula
In the simplest form, the momentum formula can be represented by the following equation:
Choosing a Control Volume
A control volume can be selected as any arbitrary volume through which fluid flows. This volume can be static, moving, and even deforming during flow. To solve any problem, we have to solve basic conservation laws in this volume. It is very important to know all relative flow velocities to the control surface. Therefore it is very important to define exactly the boundaries of the control volume during an analysis.
Example: The force acting on a deflector elbow
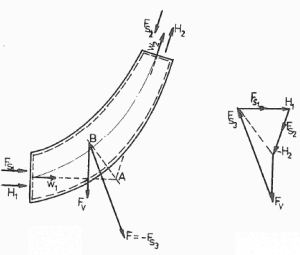 An elbow (let say of primary piping) is used to deflect water flow at a velocity of 17 m/s. The piping diameter is equal to 700 mm. The gauge pressure inside the pipe is about 16 MPa at a temperature of 290°C. Fluid is of constant density ⍴ ~ 720 kg/m3 (at 290°C). The angle of the elbow is 45°.
An elbow (let say of primary piping) is used to deflect water flow at a velocity of 17 m/s. The piping diameter is equal to 700 mm. The gauge pressure inside the pipe is about 16 MPa at a temperature of 290°C. Fluid is of constant density ⍴ ~ 720 kg/m3 (at 290°C). The angle of the elbow is 45°.
Calculate the force on the wall of a deflector elbow (i.e., calculate vector F3).
Assumptions:
- The flow is steady.
- The frictional losses are negligible.
- The weight of the elbow is negligible.
- The weight of the water in the elbow is negligible.
We take the elbow as the control volume. The control volume is shown in the picture. The momentum equation is a vector equation, so it has three components. We take the x- and z- coordinates as shown, and we will solve the problem separately according to these coordinates.
First, let us consider the component in the x-coordinate. The conservation of linear momentum equation becomes:
Second, let us consider the component in the y-coordinate. The conservation of linear momentum equation becomes:
The final force acting on the wall of a deflector elbow will be:
Example: Water Jet Striking a Stationary Plate
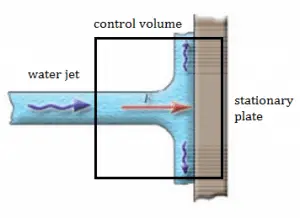 A stationary plate (e.g.,, blade of a watermill) deflects water flow at a velocity of 1 m/s and an angle of 90°. It occurs at atmospheric pressure, and the mass flow rate is equal to Q =1 m3/s.
A stationary plate (e.g.,, blade of a watermill) deflects water flow at a velocity of 1 m/s and an angle of 90°. It occurs at atmospheric pressure, and the mass flow rate is equal to Q =1 m3/s.
- Calculate the pressure force.
- Calculate the body force.
- Calculate the total force.
- Calculate the resultant force.
Solution
- The pressure force is zero as the pressure at the inlet, and the outlets to the control volume are atmospheric.
- As the control volume is small, we can ignore the body force due to the weight of gravity.
- Fx = ρ.Q.(w1x – w2x) = 1000 . 1 . (1 – 0) = 1000 N
Fy = 0
F = (1000, 0) - The resultant force on the plane is the same magnitude but in the opposite direction as the total force F (friction and weight are neglected).
The water jet exerts on the plate the force of 1000 N in the x-direction.