From a practical engineering point of view, the flow regime can be categorized according to several criteria.
All fluid flow is classified into one of two broad categories or regimes. These two flow regimes are:
- Single-phase Fluid Flow
- Multi-phase Fluid Flow (or Two-phase Fluid Flow)
This is a basic classification. All of the fluid flow equations (e.g.,, Bernoulli’s Equation) and relationships discussed in this section (Fluid Dynamics) were derived for the flow of a single phase of fluid, whether liquid or vapor. Solution of multi-phase fluid flow is very complex and difficult, and therefore it is usually in advanced courses of fluid dynamics.
 Another usually more common classification of flow regimes is according to the shape and type of streamlines. All fluid flow is classified into one of two broad categories. The fluid flow can be either laminar or turbulent, and therefore these two categories are:
Another usually more common classification of flow regimes is according to the shape and type of streamlines. All fluid flow is classified into one of two broad categories. The fluid flow can be either laminar or turbulent, and therefore these two categories are:
- Laminar Flow
- Turbulent Flow
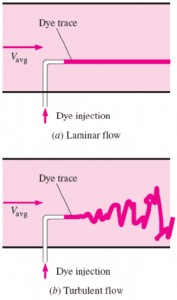
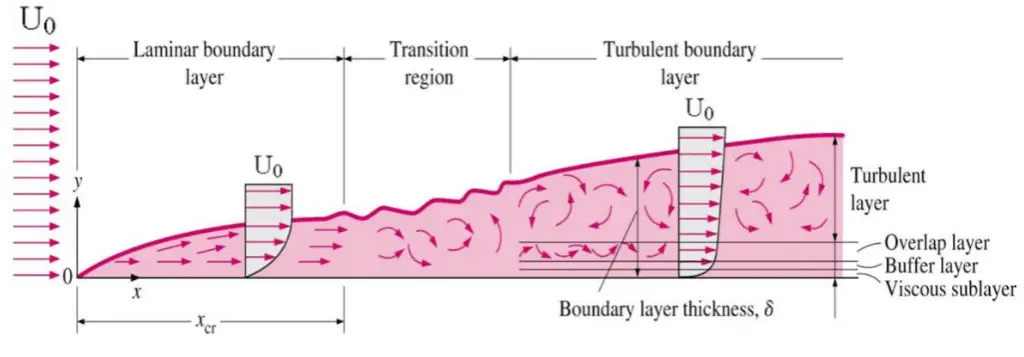
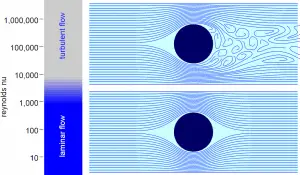
Laminar flow is characterized by smooth or regular paths of particles of the fluid. Therefore the laminar flow is also referred to as streamline or viscous flow. In contrast to laminar flow, turbulent flow is characterized by the irregular movement of particles of the fluid. The turbulent fluid does not flow in parallel layers, the lateral mixing is very high, and there is a disruption between the layers. Most industrial flows, especially those in nuclear engineering, are turbulent.
The flow regime can also be classified according to the geometry of a conduit or flow area. From this point of view, we distinguish:
- Internal Flow
- External Flow
Internal flow is a flow for which the fluid is confined by a surface. Detailed knowledge of the behavior of internal flow regimes is important in engineering because circular pipes can withstand high pressures and hence are used to convey liquids. On the other hand, external flow is such a flow in which boundary layers develop freely, without constraints imposed by adjacent surfaces. Detailed knowledge of the behavior of external flow regimes is of importance, especially in aeronautics and aerodynamics.