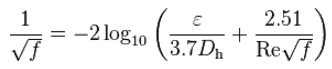Facebook Instagram Youtube Twitter

Friction Factor for Turbulent Flow – Colebrook Equation

Darcy Friction Factor for Turbulent Flow

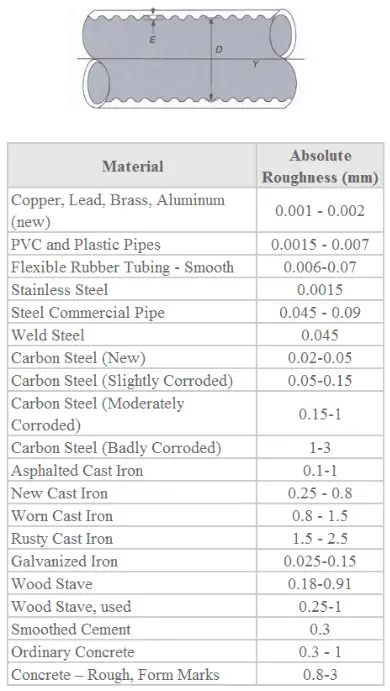
If the Reynolds number is greater than 3500, the flow is turbulent. Most fluid systems in nuclear facilities operate with turbulent flow. In this flow regime, the resistance to flow follows the Darcy–Weisbach equation: it is proportional to the square of the mean flow velocity. The Darcy friction factor depends strongly on the relative roughness of the pipe’s inner surface.

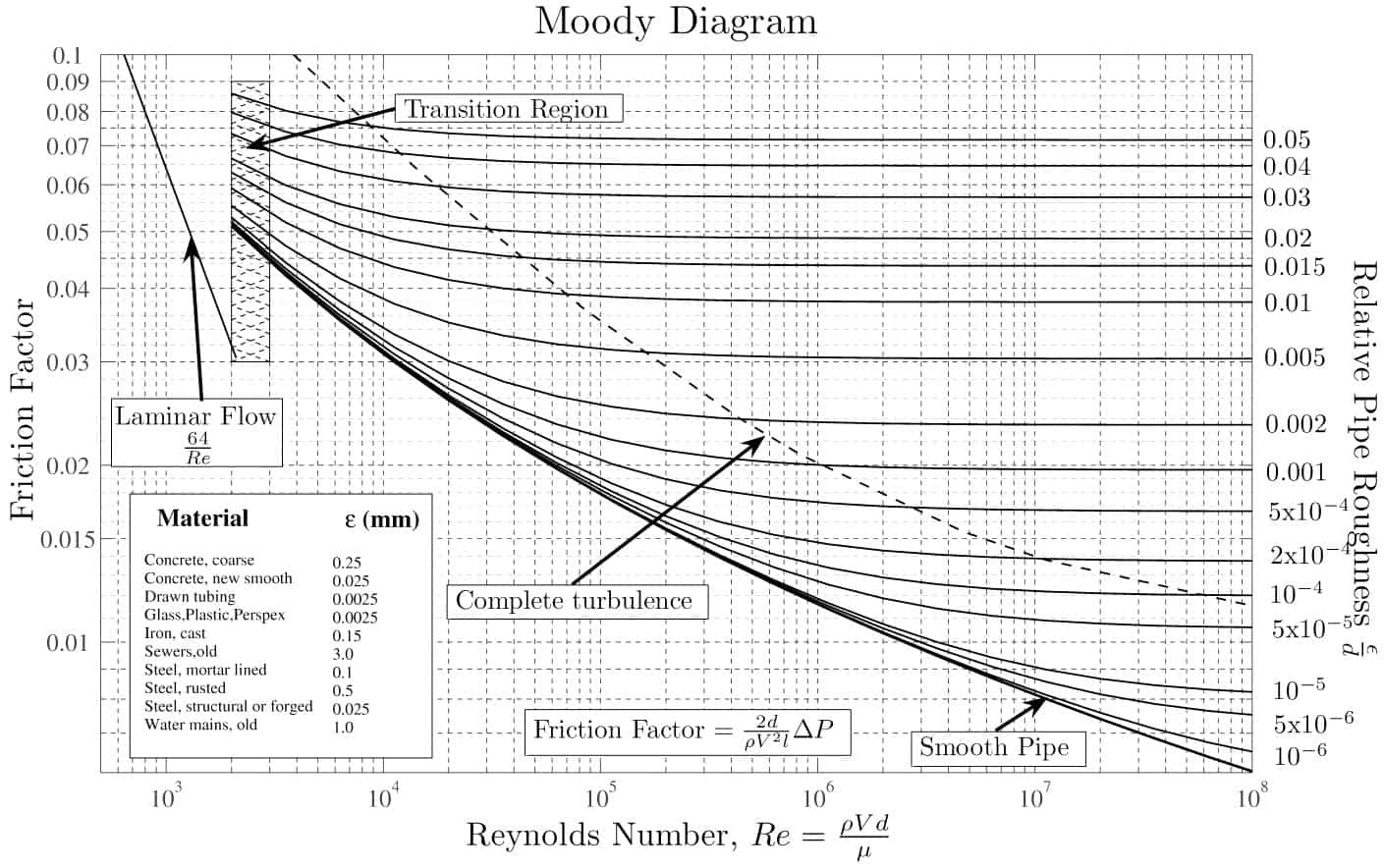
The most common method to determine a friction factor for turbulent flow is to use the Moody diagram. The Moody diagram (also known as the Moody chart) is a log-log plot of the Colebrook correlation that relates the Darcy friction factor, Reynolds number, and the relative roughness for fully developed flow in a circular pipe. The Colebrook–White equation:

darcy friction factor for turbulent flow

Turbulent Flow:
  • Re > 4000
  • ‘high’ velocity
  • The flow is characterized by the irregular movement of particles of the fluid.
  • Average motion is in the direction of the flow.
  • The flow velocity profile for turbulent flow is fairly flat across the center section of a pipe and drops rapidly extremely close to the walls.
  • The average flow velocity is approximately equal to the velocity at the center of the pipe.
  • Mathematical analysis is very difficult.
  • The most common type of flow.
which is also known as the Colebrook equation, expresses the Darcy friction factor f as a function of pipe relative roughness ε / Dh and Reynolds number.

In 1939, Colebrook found an implicit correlation for the friction factor in round pipes by fitting the data of experimental studies of turbulent flow in smooth and rough pipes.

For hydraulically smooth pipe and the turbulent flow (Re < 105), the friction factor can be approximated by the Blasius formula:

 f = (100.Re)-¼

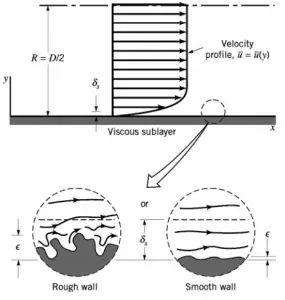darcy friction factor - relative roughnessIt must be noted that the friction factor is independent of the Reynolds number at very large Reynolds numbers. This is because the thickness of the laminar sublayer (viscous sublayer) decreases with increasing Reynolds number. For very large Reynolds numbers, the thickness of the laminar sublayer is comparable to the surface roughness, and it directly influences the flow. The laminar sublayer becomes so thin that the surface roughness protrudes into the flow. The frictional losses, in this case, are produced in the main flow primarily by the protruding roughness elements, and the contribution of the laminar sublayer is negligible.

Moody Diagram
Source: Donebythesecondlaw at the English language Wikipedia, CC BY-SA 3.0,
https://commons.wikimedia.org/w/index.php?curid=4681366
relative roughness - absolute roughness
 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See above:

Major Loss