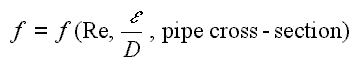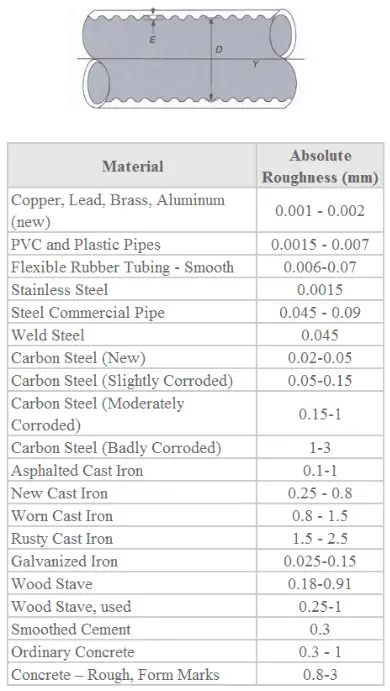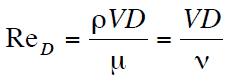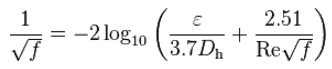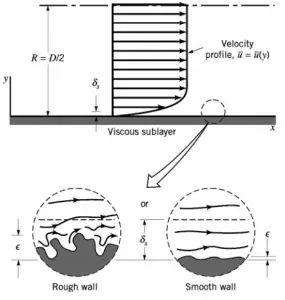
https://commons.wikimedia.org/w/index.php?curid=4681366
The friction factor has been determined to depend on the Reynolds number for the flow and the degree of roughness of the pipe’s inner surface (especially for turbulent flow). The friction factor of laminar flow is independent of the roughness of the pipe’s inner surface.
The pipe cross-section is also important, as deviations from circular cross-sections will cause secondary flows that increase the head loss. Non-circular pipes and ducts are generally treated by using the hydraulic diameter.
where both the average height surface irregularities and the pipe diameter are in millimeters.
If we know the relative roughness of the pipe’s inner surface, then we can obtain the value of the friction factor from the Moody Chart.
The Moody chart (also known as the Moody diagram) is a graph in the non-dimensional form that relates the Darcy friction factor, Reynolds number, and the relative roughness for fully developed flow in a circular pipe.
It is a dimensionless number comprised of the physical characteristics of the flow. An increasing Reynolds number indicates increasing turbulence of flow.
It is defined as:
where:
V is the flow velocity,
D is a characteristic linear dimension, (travelled length of the fluid; hydraulic diameter etc.)
ρ fluid density (kg/m3),
μ dynamic viscosity (Pa.s),
ν kinematic viscosity (m2/s); ν = μ / ρ.
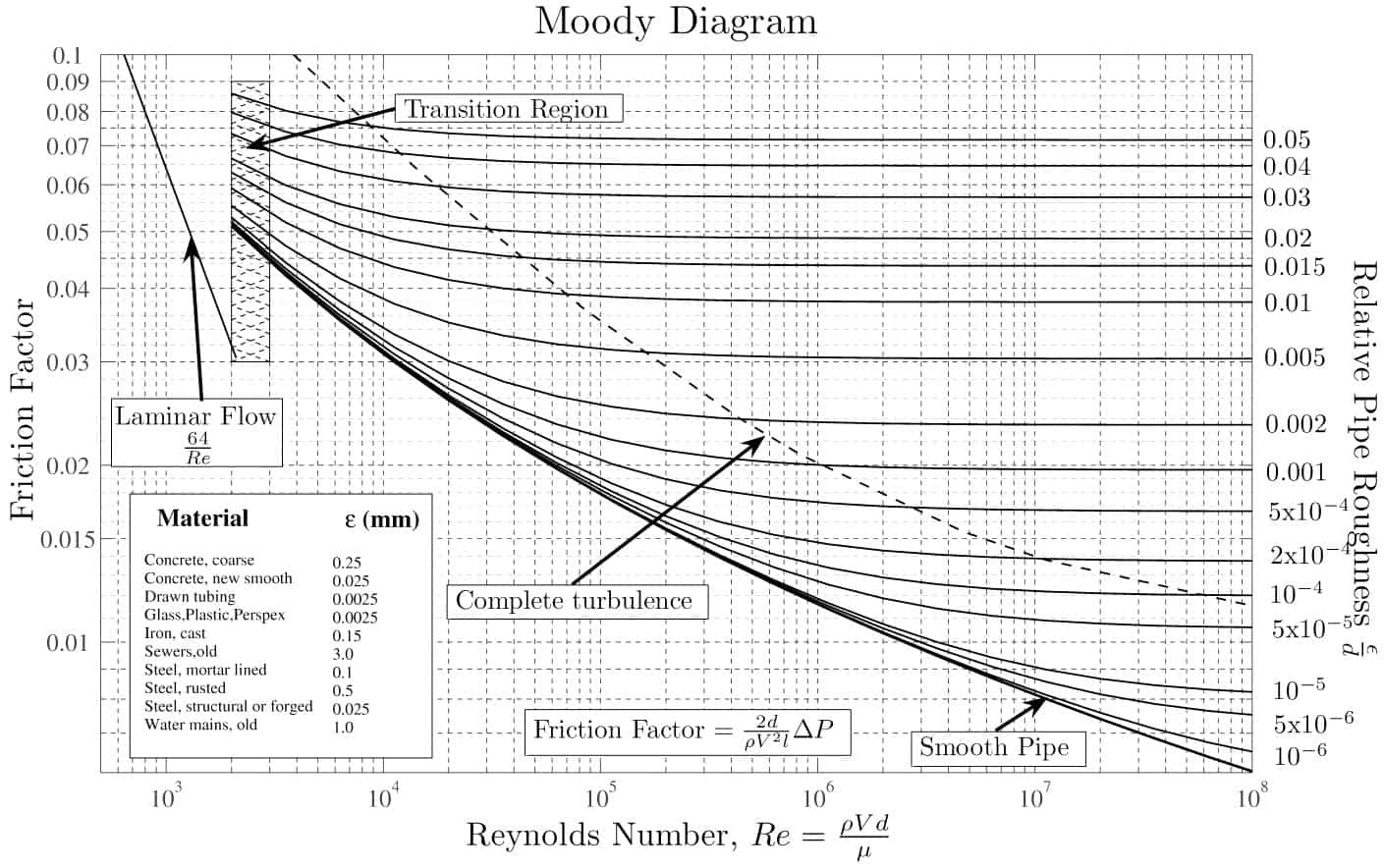
Example: Moody Diagram
Using the Moody diagram, determine the friction factor (fD) for fluid flow in a pipe of 700mm in diameter with a Reynolds number of 50 000 000 and an absolute roughness of 0.035 mm.
Solution:
The relative roughness is equal to ε = 0.035 / 700 = 5 x 10-5. Using the Moody Chart, a Reynolds number of 50 000 000 intersects the curve corresponding to a relative roughness of 5 x 10-5 at a friction factor of 0.011.
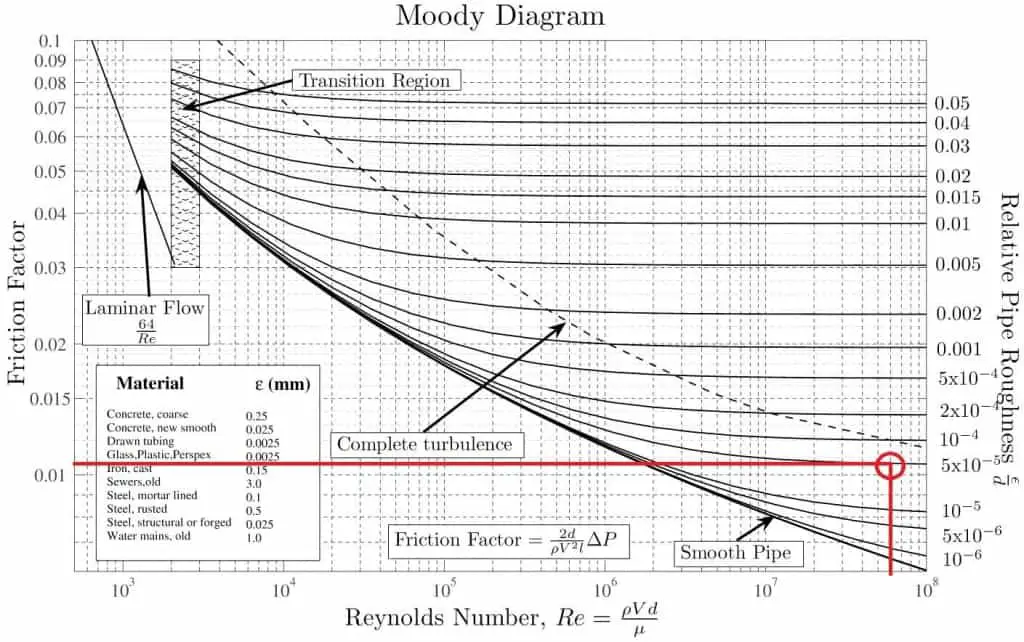
Source: Donebythesecondlaw at the English language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4681366
Darcy Friction Factor for various flow regime
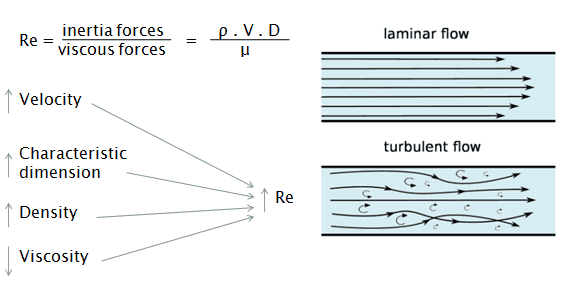
The most common classification of flow regimes is according to the Reynolds number. The Reynolds number is a dimensionless number comprised of the physical characteristics of the flow, and it determines whether the flow is laminar or turbulent. An increasing Reynolds number indicates increasing turbulence of flow. As can be seen from the Moody chart, the Darcy friction factor also depends on the flow regime (i.e., on the Reynolds number).
The Darcy friction factor for laminar (slow) flows is a consequence of Poiseuille’s law that and it is given by the following equations:
The most common method to determine a friction factor for turbulent flow is to use the Moody chart. The Moody chart (also known as the Moody diagram) is a log-log plot of the Colebrook correlation that relates the Darcy friction factor, Reynolds number, and the relative roughness for fully developed flow in a circular pipe. The Colebrook–White equation:
which is also known as the Colebrook equation, expresses the Darcy friction factor f as a function of pipe relative roughness ε / Dh and Reynolds number.
In 1939, Colebrook found an implicit correlation for the friction factor in round pipes by fitting the data of experimental studies of turbulent flow in smooth and rough pipes.
For hydraulically smooth pipe and the turbulent flow (Re < 105), the friction factor can be approximated by the Blasius formula:
f = (100.Re)-¼
It must be noted that the friction factor is independent of the Reynolds number at very large Reynolds numbers. This is because the thickness of the laminar sublayer (viscous sublayer) decreases with increasing Reynolds number. For very large Reynolds numbers, the thickness of the laminar sublayer is comparable to the surface roughness, and it directly influences the flow. The laminar sublayer becomes so thin that the surface roughness protrudes into the flow. The frictional losses, in this case, are produced in the main flow primarily by the protruding roughness elements, and the contribution of the laminar sublayer is negligible.