Facebook Instagram Youtube Twitter

Critical Reynolds Number

The critical Reynolds number is associated with the laminar-turbulent transition, in which a laminar flow becomes turbulent.

For flow in a pipe of diameter D, experimental observations show that for “fully developed” flow, the critical Reynolds number is about Red,crit = 2300.

For flow over a flat plate, transition from laminar to turbulent boundary layer occurs when Reynolds number at x exceeds Rex,crit ~ 500,000.

The Reynolds number is the ratio of inertial forces to viscous forces and is a convenient parameter for predicting if a flow condition will be laminar or turbulent.

The critical Reynolds number is associated with the laminar-turbulent transition, in which a laminar flow becomes turbulent. This is an extraordinarily complicated process, which is not fully understood at present.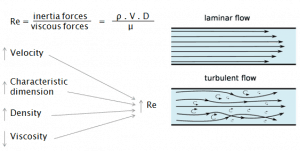reynolds number

The value of the critical Reynolds number is different for different geometries.

  • For flow over a flat plate, the generally accepted value of the critical Reynolds number is Rex ~ 500000.
  • For flow in a pipe of diameter D, experimental observations show that for “fully developed” flow, laminar flow occurs when ReD < 2300, and turbulent flow occurs when ReD > 3500.
  • For a sphere in a fluid, the characteristic length-scale is the diameter of the sphere, and the characteristic velocity is that of the sphere relative to the fluid. Purely laminar flow only exists up to Re = 10 under this definition.

Critical Reynolds Number for Flow in a Pipe

For flow in a pipe of diameter D, experimental observations show that for “fully developed” flow, the critical Reynolds number is about Red,crit = 2300.

  • Laminar flow. For practical purposes, the flow is laminar if the Reynolds number is less than 2000. The accepted transition Reynolds number for flow in a circular pipe is Red,crit = 2300.
  • Transitional flow. At Reynolds numbers between about 2000 and 4000, the flow is unstable due to the onset of turbulence. These flows are sometimes referred to as transitional flows.
  • Turbulent flow. If the Reynolds number is greater than 3500, the flow is turbulent.

Note that the critical Reynolds number is different for every geometry.

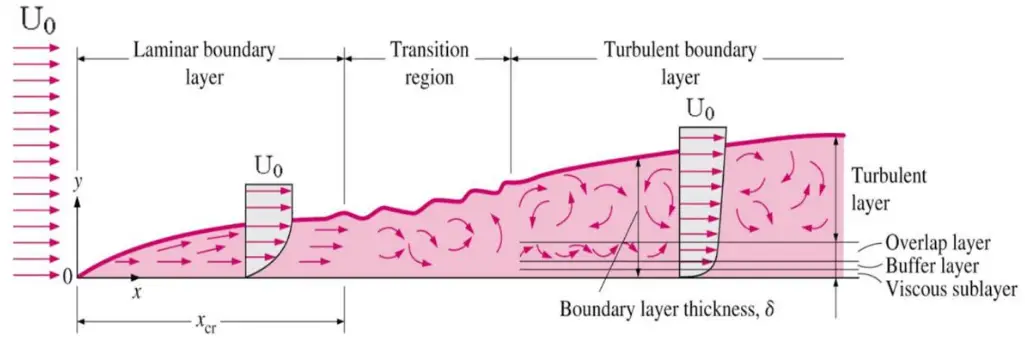
Critical Reynolds Number in boundary layer flow over a flat plate.

In determining whether the boundary layer is laminar or turbulent, it is frequently reasonable to assume that transition begins at some location xcrit, as shown in the figure. This location is determined by the critical Reynolds number, Rex,crit. For flow over a flat plate,

transition from laminar to turbulent boundary layer occurs when Reynolds number at x exceeds Rex,crit ~ 500,000. The transition may occur earlier, but it is dependent especially on the surface roughness. The turbulent boundary layer thickens more rapidly than the laminar boundary layer due to increased shear stress at the body surface.

Boundary layer on flat plate

Example: Critical Reynolds Number

A long thin flat plate is placed parallel to a 1 m/s stream of water at 20°C. Assume that the kinematic viscosity of water at 20°C is equal to 1×10-6 m2/s.

At what distance x from the leading edge will be the transition from laminar to turbulent boundary layer (i.e., find Rex ~ 500,000).

Solution:

To locate the transition from laminar to the turbulent boundary layer, we have to find x at Rex ~ 500,000.

x = 500 000 x 1×10-6 [m2/s] / 1 [m/s] = 0.5 m

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Reynolds Number