The Reynolds number represents the ratio of inertial forces to viscous forces and is a convenient parameter for predicting if a flow condition will be laminar or turbulent. It is defined as a characteristic length multiplied by a characteristic velocity and divided by the kinematic viscosity.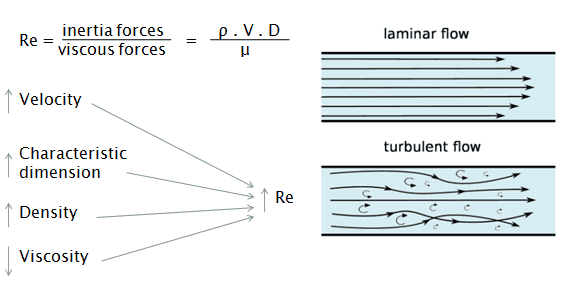
It can be interpreted that when the viscous forces are dominant (slow flow, low Re), they are sufficient enough to keep all the fluid particles in line, then the flow is laminar. Even very low Re indicates viscous creeping motion, where inertia effects are negligible. When the inertial forces dominate the viscous forces (when the fluid is flowing faster and Re is larger), the flow is turbulent. The transition from laminar to turbulent flow depends on the surface geometry, surface roughness, free-stream velocity, surface temperature, and fluid type, among other things.
History of Reynolds Number
George Stokes introduced the concept in 1851, but Arnold Sommerfeld named the Reynolds number in 1908 after Osborne Reynolds (1842–1912), who performed exhaustive experiments in the 1880s. Osborn Reynolds discovered that the flow regime depends mainly on the ratio of the inertia forces to viscous forces in the fluid.

This study is closely associated with the boundary layer concept. The study of flows developing along a solid boundary is of primary importance for many engineering problems, such as the drag reduction of airplane wings in the aeronautics field. In the boundary layer concept, introduced by Prandtl (1904), the field of wall-bounded flows can be divided into two regions:
- a thin region near the wall called the boundary layer, where strong velocity gradients occur, inducing large viscous shearing forces that must be taken into account and
- a region outside the boundary layer, where the friction forces can be neglected and where, therefore, inviscid fluid theory offers a good approximation.
The major contribution of the boundary layer concept was to overcome the D’Alembert paradox and reunify theoretical hydrodynamics (derived in the framework of the perfect fluid hypothesis) with empirical laws from hydraulics. Fundamental research on boundary layers is focused on studying canonical configurations such as pipe flow, channel flow, or flow over a flat plate.
The flow over a flat plate can be seen near the leading edge of the plate. The régime of the boundary layer is laminar: the flow is two-dimensional and steady. As the boundary layer develops, the flow becomes critical and undergoes a transition from the laminar to the turbulent regime: instabilities appear and propagate, giving birth to turbulent spots irregularly distributed in space and time. As the distance x from the leading edge increases (i.e., as the Reynolds Number increases), the flow becomes unstable, and finally, for higher Reynolds numbers, the boundary layer is turbulent, and the streamwise velocity is characterized by unsteady (changing with time) swirling flows inside the boundary layer. Turbulence always occurs at large Reynolds numbers.