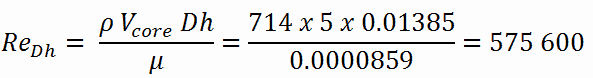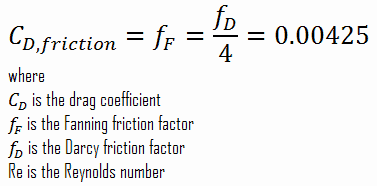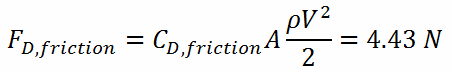Drag Force in Nuclear Engineering
Analysis of the hydraulic lift force is one of the most important analyses in designing a fuel assembly and analyzing the hydraulic compatibility of mixed cores. The vertical forces are induced by upward high-velocity flow through the reactor core, and the flow path for the reactor coolant through the reactor vessel would be:
-
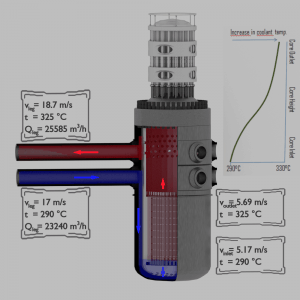
Example of flow rates in a reactor. It is an illustrative example, and the data do not represent any reactor design. The coolant enters the reactor vessel at the inlet nozzle and hits against the core barrel.
- The core barrel forces the water to flow downward in the space between the reactor vessel wall and the core barrel, and this space is usually known as the downcomer.
- The flow is reversed up through the core from the bottom of the pressure vessel to pass through the fuel assemblies, where the coolant temperature increases as it passes through the fuel rods.
- Finally, the hotter reactor coolant enters the upper internals region, where it is routed out the outlet nozzle into the hot legs of the primary circuit and goes on to the steam generators.
Fuel assemblies are held by the upper guide structure assembly, which defines the top of the core. This assembly is made of stainless steel and has many purposes. The upper guide structure assembly exerts an axial force on fuel assemblies (through springs in the top nozzle), thus defining the exact position of the fuel assembly in the core. The upper guide structure assembly flange is held in place and preloaded by the RPV closure head flange. The upper guide structure assembly also guides and protects control rod assemblies and in-core instrumentation.
Required downforce of the upper guide structure assembly on fuel assemblies must very carefully calculated. Insufficient downforce can result in the lift of the fuel assembly, on the other hand, an excessive downforce can result in bowing of fuel assembly, which is also unacceptable.
Example: Drag Force – Drag Coefficient – Fuel Bundle
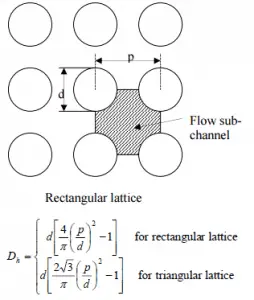Calculate the friction drag of a single fuel rod inside a reactor core at normal operation (design flow rate). Assume that this fuel rod is part of a fuel bundle with the rectangular fuel lattice, and this fuel bundle does not contain spacing grids. Its height is h = 4m, and the core flow velocity is constant and equal to Vcore = 5 m/s.
Assume that:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the pitch of fuel pins is: p = 13 mm
- the relative roughness is ε/D = 5×10-4
- the fluid density is: ρ = 714 kg/m3
- the core flow velocity is constant and equal to Vcore = 5 m/s
- the average temperature of reactor coolant is: Tbulk = 296°C
Calculation of the Reynolds number
To calculate the Reynolds number, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm (to calculate the hydraulic diameter)
- the pitch of fuel pins is: p = 13 mm (to calculate the hydraulic diameter)
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the fluid density is: ρ = 714 kg/m3
The hydraulic diameter, Dh, is a commonly used term when handling flow in non-circular tubes and channels. The hydraulic diameter of the fuel channel, Dh, is equal to 13,85 mm.
See also: Hydraulic Diameter
The Reynolds number inside the fuel channel is then equal to:
This fully satisfies the turbulent conditions.
Calculation of the Skin Friction Coefficient
The friction factor for turbulent flow depends strongly on the relative roughness. It is determined by the Colebrook equation or can be determined using the Moody chart. The Moody chart for Re = 575 600 and ε/D = 5 x 10-4 returns following values:
- the Darcy friction factor is equal to fD = 0.017
- the Fanning friction factor is equal to fF = fD/4 = 0.00425
Therefore the skin friction coefficient is equal to:
Calculation of the Drag Force
To calculate the drag force, we have to know:
- the skin friction coefficient, which is: CD,friction = 0.00425
- the area of pin surface, which is: A = π.d.h = 0.1169 m2
- the fluid density, which is: ρ = 714 kg/m3
- the core flow velocity, which is constant and equal to Vcore = 5 m/s
From the skin friction coefficient, which is equal to the Fanning friction factor, we can calculate the frictional component of the drag force. The drag force is given by:
Assuming that a fuel assembly can have, for example, 289 fuel pins (17×17 fuel assembly), the frictional component of the drag force is then of the order of kilonewtons. Moreover, this drag force originates purely from the skin friction on the fuel bundle. But typical PWR fuel assembly contains other components which influence the fuel assembly hydraulics:
- Fuel rods. Fuel rods contain fuel and burnable poisons.
- Top nozzle. Provides the mechanical support for the fuel assembly structure.
- Bottom nozzle. Provides the mechanical support for the fuel assembly structure.
- Spacing grid. Ensures an exact guiding of the fuel rods.
- Guide thimble tube. Vacant tube for control rods or in-core instrumentation.
As was written, the second component of the drag force is the form drag. Form drag, also known as pressure drag, arises because of the shape and size of the object. The pressure drag is proportional to the difference between the pressures acting on the front and back of the immersed body and the frontal area.
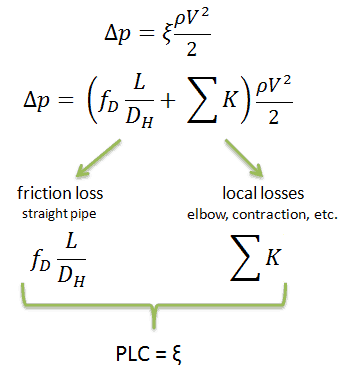
Pressure Drop – Fuel Assembly
In general, total fuel assembly pressure drop is formed by fuel bundle frictional drop (dependent on relative roughness of fuel rods, Reynolds number, hydraulic diameter, etc.) and other pressure drops of structural elements (top and bottom nozzle, spacing grids, or mixing grids).
In general, it is not so simple to calculate pressure drops in fuel assemblies (especially the spacing grids), and it belongs to the key know-how of certain fuel manufacturers. Mostly, pressure drops are measured in experimental hydraulic loops rather than calculated.
Engineers use the pressure loss coefficient, PLC. It is noted K or ξ (pronounced “xi”). This coefficient characterizes pressure loss of a certain hydraulic system or a part of a hydraulic system, and it can be easily measured in hydraulic loops. The pressure loss coefficient can be defined or measured for both straight pipes and especially for local (minor) losses.
Using data from the example mentioned above, the pressure loss coefficient (only frictional from the straight pipe) is equal to ξ = fDL/DH = 4.9. But the overall pressure loss coefficient (including spacing grids, top, and bottom nozzles, etc.) is usually about three times higher. This PLC (ξ = 4.9) causes the pressure drop to be of the order of (using the previous inputs) Δpfriction = 4.9 x 714 x 52/ 2 = 43.7 kPa (without spacing grids, top, and bottom nozzles). About three times higher real PLC means about three times higher Δpfuel will be.
The overall reactor pressure loss, Δpreactor, must include:
- downcomer and reactor bottom
- lower support plate
- fuel assembly including spacing grids, top and bottom nozzles, and other structural components – Δpfuel
- upper guide structure assembly
As a result, the overall reactor pressure loss – Δpreactor is usually of the order of hundreds kPa (let’s say 300 – 400 kPa) for design parameters.
