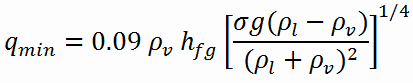Film boiling occurs when the pressure of a system drops or the flow decreases. In this case, the bubbles cannot escape as quickly from the heat transfer surface. Likewise, if the temperature of the heat transfer surface is increased, more bubbles are created. As the temperature increases, more bubbles are formed than can be efficiently carried away. The bubbles grow and group together, covering small areas of the heat transfer surface with a film of steam.
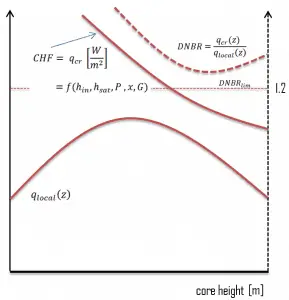
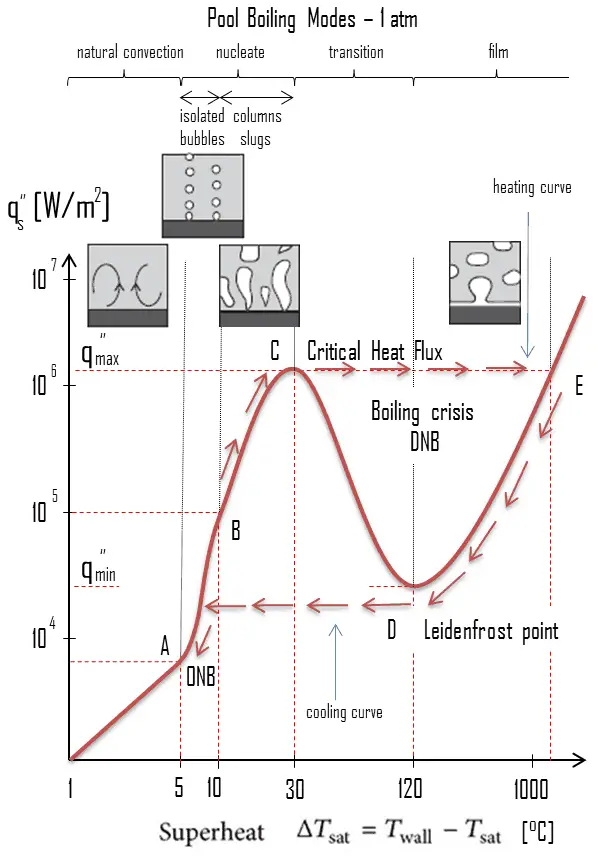
The nucleate boiling heat flux cannot be increased indefinitely. We call it the “critical heat flux” (CHF) at some value. The steam produced can form an insulating layer over the surface, which in turn deteriorates the heat transfer coefficient. This is because a large fraction of the surface is covered by a vapor film, which acts as thermal insulation due to the low thermal conductivity of the vapor relative to that of the liquid. Immediately after the critical heat flux has been reached, boiling becomes unstable, and transition boiling occurs. The transition from nucleate boiling to film boiling is known as the “boiling crisis”. Since the heat transfer coefficient decreases beyond the CHF point, the transition to film boiling is usually inevitable.
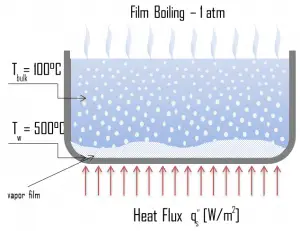
A further increase in the heat flux causes a film of vapor to cover the surface fully. This significantly reduces the convection coefficient since the vapor layer has significantly lower heat transfer ability. As a result, the excess temperature shoots up to a very high value. Beyond the Leidenfrost point, a continuous vapor film blankets the surface, and there is no contact between the liquid phase and the surface. In this situation, the heat transfer is both by radiation and conduction to the vapor.
If the material is not strong enough for withstanding this temperature, the equipment will fail by damage to the material. This phenomenon is also known as burnout. In pressurized water reactors, one of the key safety requirements (maybe the most important) is that a departure from nucleate boiling (DNB) will not occur during steady-state operation, normal operational transients, and anticipated operational occurrences (AOOs). Fuel cladding integrity will be maintained if the minimum DNBR remains above the 95/95 DNBR limit for PWRs ( a 95% probability at a 95% confidence level). Since this phenomenon deteriorates the heat transfer coefficient and the heat flux remains, heat accumulates in the fuel rod, causing the dramatic rise of cladding and fuel temperature. Simply, a very high-temperature difference is required to transfer the critical heat flux produced from the fuel rod’s surface to the reactor coolant (through the vapor layer).
Film boiling occurs when the pressure of a system drops or the flow decreases. In this case, the bubbles cannot escape as quickly from the heat transfer surface. Likewise, if the temperature of the heat transfer surface is increased, more bubbles are created. As the temperature increases, more bubbles are formed than can be efficiently carried away. The bubbles grow and group together, covering small areas of the heat transfer surface with a film of steam. This is known as partial film boiling.
The following sections describe:
- Transition to Film Boiling – Critical Heat Flux
- Departure from Film Boiling – Leidenfrost Point
Boiling Crisis – Critical Heat Flux
 As was written, in nuclear reactors, limitations of the local heat flux are of the highest importance for reactor safety. For pressurized water reactors and boiling water reactors, there are thermal-hydraulic phenomena, which cause a sudden decrease in heat transfer efficiency (more precisely in the heat transfer coefficient). These phenomena occur at a certain value of heat flux, known as the “critical heat flux”. The phenomena that cause heat transfer deterioration are different for PWRs and BWRs.
As was written, in nuclear reactors, limitations of the local heat flux are of the highest importance for reactor safety. For pressurized water reactors and boiling water reactors, there are thermal-hydraulic phenomena, which cause a sudden decrease in heat transfer efficiency (more precisely in the heat transfer coefficient). These phenomena occur at a certain value of heat flux, known as the “critical heat flux”. The phenomena that cause heat transfer deterioration are different for PWRs and BWRs.
In both types of reactors, the problem is more or less associated with departure from nucleate boiling. The nucleate boiling heat flux cannot be increased indefinitely, and we call it the “critical heat flux” (CHF) at some value. The steam produced can form an insulating layer over the surface, which in turn deteriorates the heat transfer coefficient. Immediately after the critical heat flux has been reached, boiling becomes unstable, and film boiling occurs. The transition from nucleate boiling to film boiling is known as the “boiling crisis”. As was written, the phenomena that cause heat transfer deterioration are different for PWRs and BWRs.
Departure From Nucleate Boiling – DNB
 In the case of PWRs, the critical safety issue is named DNB (departure from nucleate boiling), which causes the formation of a local vapor layer, causing a dramatic reduction in heat transfer capability. This phenomenon occurs in the subcooled or low-quality region. The behavior of the boiling crisis depends on many flow conditions (pressure, temperature, flow rate). Still, the boiling crisis occurs at relatively high heat fluxes and appears to be associated with the cloud of bubbles adjacent to the surface. These bubbles or films of vapor reduce the amount of incoming water. Since this phenomenon deteriorates the heat transfer coefficient and the heat flux remains, heat accumulates in the fuel rod, causing the dramatic rise of cladding and fuel temperature. Simply, a very high-temperature difference is required to transfer the critical heat flux being produced from the surface of the fuel rod to the reactor coolant (through the vapor layer).
In the case of PWRs, the critical safety issue is named DNB (departure from nucleate boiling), which causes the formation of a local vapor layer, causing a dramatic reduction in heat transfer capability. This phenomenon occurs in the subcooled or low-quality region. The behavior of the boiling crisis depends on many flow conditions (pressure, temperature, flow rate). Still, the boiling crisis occurs at relatively high heat fluxes and appears to be associated with the cloud of bubbles adjacent to the surface. These bubbles or films of vapor reduce the amount of incoming water. Since this phenomenon deteriorates the heat transfer coefficient and the heat flux remains, heat accumulates in the fuel rod, causing the dramatic rise of cladding and fuel temperature. Simply, a very high-temperature difference is required to transfer the critical heat flux being produced from the surface of the fuel rod to the reactor coolant (through the vapor layer).
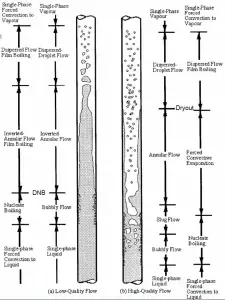
In the case of PWRs, the critical flow is inverted annular flow, while in BWRs, the critical flow is usually annular flow. The difference in flow regime between post-dry-out flow and post-DNB flow is depicted in the figure. In PWRs at normal operation, the flow is considered to be single-phase. But a great deal of study has been performed on the nature of two-phase flow in case of transients and accidents (such as the loss-of-coolant accident – LOCA or trip of RCPs), which are of importance in reactor safety and in must be proved and declared in the Safety Analysis Report (SAR).
One of the key safety requirements of pressurized water reactors is that a departure from nucleate boiling (DNB) will not occur during steady-state operation, normal operational transients, and anticipated operational occurrences (AOOs). Fuel cladding integrity will be maintained if the minimum DNBR remains above the 95/95 DNBR limit for PWRs ( a 95% probability at a 95% confidence level). DNB criterion is one of the acceptance criteria in safety analyses as well as it constitutes one of the safety limits in technical specifications.
Dryout – BWRs
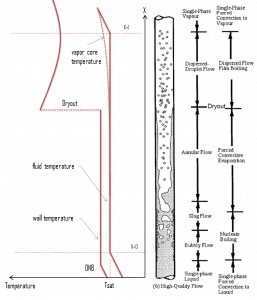 In BWRs, a similar phenomenon is known as “dry out,” and it is directly associated with changes in flow pattern during evaporation in the high-quality region. At given combinations of flow rate through a channel, pressure, flow quality, and linear heat rate, the liquid wall film may exhaust, and the wall may be dried out. At normal, the fuel surface is effectively cooled by boiling coolant. However, when the heat flux exceeds a critical value (CHF – critical heat flux), the flow pattern may reach the dry-out conditions (the thin film of liquid disappears). The heat transfer from the fuel surface into the coolant is deteriorated due to a drastically increased fuel surface temperature. In the high-quality region, the crisis occurs at a lower heat flux. Since the flow velocity in the vapor core is high, post-CHF heat transfer is much better than low-quality critical flux (i.e., for PWRs, temperature rises are higher and more rapid).
In BWRs, a similar phenomenon is known as “dry out,” and it is directly associated with changes in flow pattern during evaporation in the high-quality region. At given combinations of flow rate through a channel, pressure, flow quality, and linear heat rate, the liquid wall film may exhaust, and the wall may be dried out. At normal, the fuel surface is effectively cooled by boiling coolant. However, when the heat flux exceeds a critical value (CHF – critical heat flux), the flow pattern may reach the dry-out conditions (the thin film of liquid disappears). The heat transfer from the fuel surface into the coolant is deteriorated due to a drastically increased fuel surface temperature. In the high-quality region, the crisis occurs at a lower heat flux. Since the flow velocity in the vapor core is high, post-CHF heat transfer is much better than low-quality critical flux (i.e., for PWRs, temperature rises are higher and more rapid).
Departure from Film Boiling – Leidefrost Point
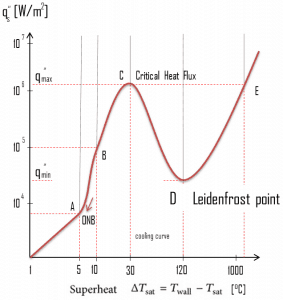 The Leidenfrost point, which corresponds to the minimal heat flux, is of practical interest since it represents the lower limit for the heat flux in the film boiling regime. If the heat flux drops below this minimum, the film will collapse, causing the surface to cool and nucleate boiling to be reestablished. Therefore, return to nucleate boiling (RNB) occurs at this point. The terms quenching, minimum heat flux, return to nucleate boiling, departure from film boiling, film boiling collapse, and Leidenfrost point have been used interchangeably to refer to various forms of rewetting, but they are not exactly synonymous.
The Leidenfrost point, which corresponds to the minimal heat flux, is of practical interest since it represents the lower limit for the heat flux in the film boiling regime. If the heat flux drops below this minimum, the film will collapse, causing the surface to cool and nucleate boiling to be reestablished. Therefore, return to nucleate boiling (RNB) occurs at this point. The terms quenching, minimum heat flux, return to nucleate boiling, departure from film boiling, film boiling collapse, and Leidenfrost point have been used interchangeably to refer to various forms of rewetting, but they are not exactly synonymous.
Using the stability theory, Zuber derived the following expression for the minimum heat flux (and corresponding Leidenfrost point) for a large horizontal plate:
where
- qmin – minimal heat flux [W/m2]
- hfg – enthalpy of vaporization, J/kg
- g – gravitational acceleration m/s2
- ρl — density of the liquid kg/m3
- ρv — density of vapor kg/m3
- σ — surface tension-liquid-vapor interface N/m
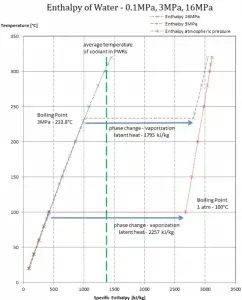
 The change from the liquid to the vapor state due to boiling is sustained by heat transfer from the solid surface; conversely, condensation of a vapor to the liquid state results in heat transfer to the solid surface. Boiling and condensation differ from other forms of convection in that they depend on the latent heat of vaporization, which is very high for common
The change from the liquid to the vapor state due to boiling is sustained by heat transfer from the solid surface; conversely, condensation of a vapor to the liquid state results in heat transfer to the solid surface. Boiling and condensation differ from other forms of convection in that they depend on the latent heat of vaporization, which is very high for common