Natural Convection Boiling

Natural convection boiling occurs when ΔTsat < 5°C. In this boiling mode, vapor will be observed over the water surface, but usually, no bubbles will be observed. As the superheat temperature increases, bubble inception will eventually occur, but below point A, fluid motion is determined principally by natural convection currents.

Categorization by the wall superheat temperature, ΔT_sat:

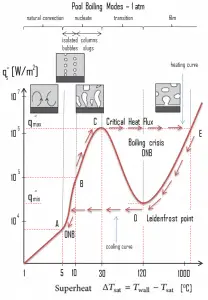The pioneering work on boiling was done in 1934 by S. Nukiyama, who used electrically heated nichrome and platinum wires immersed in liquids in his experiments. Nukiyama was the first to identify different regimes of pool boiling using his apparatus. He noticed that boiling takes different forms, depending on the value of the wall superheat temperature ΔT_sat (also known as the excess temperature), defined as the difference between the wall temperature, T_wall, and the saturation temperature, T_sat.

Four different boiling regimes of pool boiling (based on the excess temperature) are observed:

Natural Convection Boiling ΔT_sat < 5°C
Nucleate Boiling 5°C < ΔT_sat < 30°C
Transition Boiling 30°C < ΔT_sat < 200°C
Film Boiling 200°C < ΔT_sat

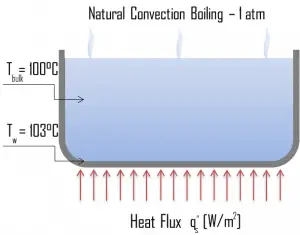In thermodynamics, the requirement for boiling of pure substances to occur is that T_wall = T_sat. But in real experiments, boiling does not occur until the liquid is heated a few degrees above the saturation temperature. To sustain vapor formation, the surface temperature must be somewhat above the saturation temperature. Natural convection boiling occurs when ΔTsat < 5°C. In this boiling mode, vapor will be observed over the water surface, but usually, no bubbles will be observed. As the superheat temperature increases, bubble inception will eventually occur, but below point A, fluid motion is determined principally by natural convection currents. Point A is usually referred to as the onset of nucleate boiling – ONB.

Boiling Point - Saturation

In thermodynamics, the term saturation defines a condition in which a mixture of vapor and liquid can exist together at a given temperature and pressure. The temperature at which vaporization (boiling) occurs for a given pressure is called the saturation temperature or boiling point. The pressure at which vaporization (boiling) occurs for a given temperature is called the saturation pressure.

When the vapor quality is equal to 0, it is referred to as the saturated liquid state (single-phase). On the other hand, when the vapor quality is equal to 1, it is referred to as the saturated vapor state or dry steam (single-phase). We talk about a vapor-liquid mixture or wet steam (two-phase mixture) between these two states. At constant pressure, the addition of energy does not change the mixture’s temperature, but the vapor quality and specific volume change.

Boiling

Phase diagram of water.
Source: wikipedia.org CC BY-SA

We have discussed convective heat transfer in the preceding chapters with a very important assumption, and we have assumed a single-phase convective heat transfer without any phase change. This chapter focuses on convective heat transfer associated with the change in phase of a fluid. In particular, we consider processes that can occur at a solid-liquid or solid–vapor interface, namely, boiling (liquid-to-vapor phase change) and condensation (vapor-to-liquid phase change).

Latent heat effects associated with the phase change are significant for these cases. Latent heat, also known as the enthalpy of vaporization, is the amount of heat added to or removed from a substance to produce a phase change. This energy breaks down the intermolecular attractive forces and must provide the energy necessary to expand the gas (the pΔV work). When latent heat is added, no temperature change occurs.

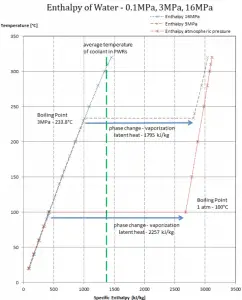
Latent heat of vaporization - water at 0.1 MPa, 3 MPa, 16 MPa — The heat of vaporization diminishes with increasing pressure while the boiling point increases, and it vanishes completely at a certain point called the critical point.

The enthalpy of vaporization is a function of the pressure at which that transformation takes place.

Latent heat of vaporization – water at 0.1 MPa (atmospheric pressure)

h_lg = 2257 kJ/kg

Latent heat of vaporization – water at 3 MPa

h_lg = 1795 kJ/kg

Latent heat of vaporization – water at 16 MPa (pressure inside a pressurizer)

h_lg = 931 kJ/kg

The heat of vaporization diminishes with increasing pressure while the boiling point increases, and it vanishes completely at a certain point called the critical point. Above the critical point, the liquid and vapor phases are indistinguishable, and the substance is called a supercritical fluid.

supercritical-phase-critical-point-min The change from the liquid to the vapor state due to boiling is sustained by heat transfer from the solid surface; conversely, condensation of a vapor to the liquid state results in heat transfer to the solid surface. Boiling and condensation differ from other forms of convection in that they depend on the latent heat of vaporization, which is very high for common pressures. Therefore large amounts of heat can be transferred during boiling and condensation essentially at a constant temperature. Heat transfer coefficients, h, associated with boiling and condensation are typically much higher than those encountered in other forms of convection processes that involve a single phase.

This is due to the fact even in a turbulent flow. There is a stagnant fluid film layer (laminar sublayer) that isolates the surface of the heat exchanger. This stagnant fluid film layer plays a crucial role in the convective heat transfer coefficient. It is observed that the fluid comes to a complete stop at the surface and assumes a zero velocity relative to the surface. This phenomenon is known as the no-slip condition, and therefore, at the surface, energy flow occurs purely by conduction. But in the next layers, both conduction and diffusion-mass movement occur at the molecular or macroscopic levels. Due to the mass movement, the rate of energy transfer is higher. As was written, nucleate boiling at the surface effectively disrupts this stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid.

References:

Heat Transfer:

Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Boiling and Condensation