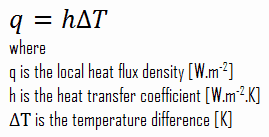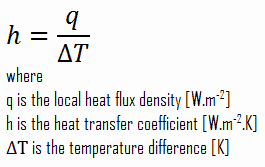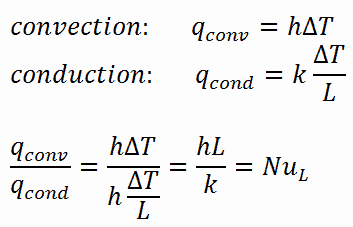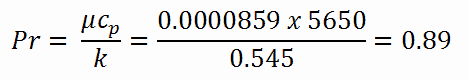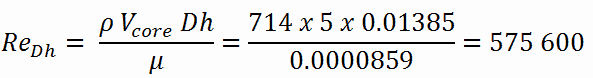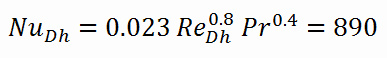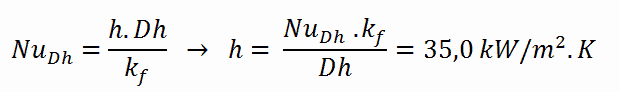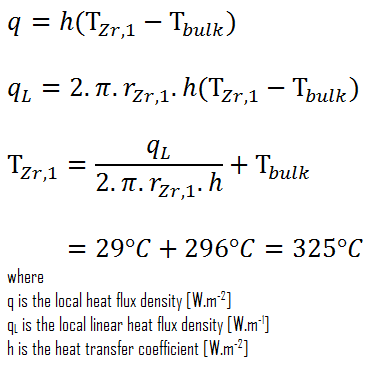Article Summary & FAQs
What is convection?
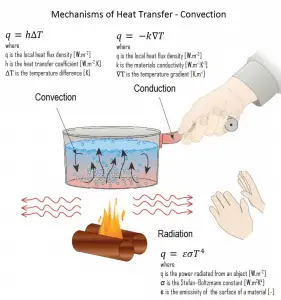
In general, convection is either the mass transfer or the heat transfer due to the bulk movement of molecules within fluids such as gases and liquids.
Key Facts
Heat transfer is usually classified into various mechanisms, such as:
-
- Heat Conduction. Heat conduction, also called diffusion, occurs within a body or between two bodies in contact. It is the direct microscopic exchange of kinetic energy of particles through the boundary between two systems.
- Heat Convection. Heat convection depends on a mass movement from one region of space to another. Heat convection occurs when the bulk flow of a fluid (gas or liquid) carries heat along with the flow of matter in the fluid.
- Thermal Radiation. Radiation is heat transfer by electromagnetic radiation, such as sunshine, with no need for the matter to be present in the space between bodies.
Conduction and convection are similar in that both mechanisms require the presence of a material medium (in comparison to thermal radiation).
At the surface, it must be emphasized that energy flow occurs purely by conduction, even in conduction. It is because there is always a thin stagnant fluid film layer on the heat transfer surface. But in the next layers, both conduction and diffusion-mass movement occur at the molecular or macroscopic levels.
Despite the complexity of convection, the rate of convection heat transfer is observed to be proportional to the temperature difference and is conveniently expressed by Newton’s law of cooling.
Newton’s law of cooling states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its surroundings, provided the temperature difference is small and the nature of radiating surface remains the same.
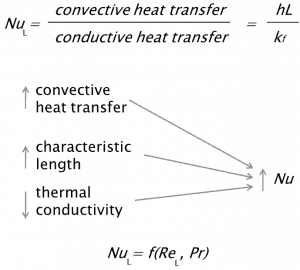
The Nusselt number is used to describe the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid.
For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus-Boelter equation.
Boiling and condensation differ from other forms of convection in that they depend on the latent heat of vaporization, which is very high for common pressures. Therefore large amounts of heat can be transferred during boiling and condensation essentially at a constant temperature.
In general, convection is either the mass transfer or the heat transfer due to the bulk movement of molecules within fluids such as gases and liquids. Although liquids and gases are generally not very good conductors of heat, they can transfer heat quite rapidly by convection.
Convection takes place through advection, diffusion, or both. Convection cannot occur in most solids because neither significant diffusion of matter nor bulk current flows can occur. Diffusion of heat occurs in rigid solids, but that is called thermal conduction.
The process of heat transfer between a surface and a fluid flowing in contact with it is called convective heat transfer. In engineering, convective heat transfer is one of the major mechanisms of heat transfer. When heat is transferred from one fluid to another through a barrier, convection is involved on both sides of the barrier. In most cases, the main resistance to heat flow is by convection. Convective heat transfer takes place both by thermal diffusion (the random motion of fluid molecules) and by advection, in which matter or heat is transported by the larger-scale motion of currents in the fluid.
Mechanisms of Convection
In thermal conduction, energy is transferred as heat either due to the migration of free electrons or lattice vibrational waves (phonons). There is no movement of mass in the direction of energy flow, and heat transfer by conduction depends on the driving “force” of temperature difference. Conduction and convection are similar in that both mechanisms require the presence of a material medium (in comparison to thermal radiation). On the other hand, they are different in that convection requires the presence of fluid motion.
At the surface, it must be emphasized that energy flow occurs purely by conduction, even in conduction. It is because there is always a thin stagnant fluid film layer on the heat transfer surface. But in the next layers, both conduction and diffusion-mass movement occur at the molecular or macroscopic levels. Due to the mass movement, the rate of energy transfer is higher. The higher the mass movement rate, the thinner the stagnant fluid film layer will be, and the higher the heat flow rate.
It must be noted nucleate boiling at the surface effectively disrupts this stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid.
As was written, heat transfer through a fluid is by convection in the presence of mass movement and conduction in its absence. Therefore, thermal conduction in a fluid can be viewed as the limiting case of convection, corresponding to the case of quiescent fluid.
Convection as a Conduction with Fluid Motion
Some experts do not consider convection to be a fundamental mechanism of heat transfer since it is essentially heat conduction in the presence of fluid motion. They consider it to be a special case of thermal conduction, known as “conduction with fluid motion”. On the other hand, it is practical to recognize convection as a separate heat transfer mechanism despite the valid arguments to the contrary.
Basic characteristics of all laminar and turbulent boundary layers are shown in the developing flow over a flat plate. The stages of the formation of the boundary layer are shown in the figure below:
Boundary layers may be either laminar or turbulent, depending on the value of the Reynolds number.
See also: Boundary Layer
Similarly, as a velocity boundary layer develops when there is fluid flow over a surface, a thermal boundary layer must develop if the bulk temperature and surface temperature differ. Consider flow over an isothermal flat plate at a constant temperature of Twall. At the leading edge, the temperature profile is uniform with Tbulk. Fluid particles that come into contact with the plate achieve thermal equilibrium at the plate’s surface temperature. At this point, energy flow occurs at the surface purely by conduction. These particles exchange energy with those in the adjoining fluid layer (by conduction and diffusion), and temperature gradients develop in the fluid. The region of the fluid in which these temperature gradients exist is the thermal boundary layer. Its thickness, δt, is typically defined as the distance from the body at which the temperature is 99% of the temperature found from an inviscid solution. With increasing distance from the leading edge, the effects of heat transfer penetrate farther into the stream, and the thermal boundary layer grows.
The ratio of these two thicknesses (velocity and thermal boundary layers) is governed by the Prandtl number, defined as the ratio of momentum diffusivity to thermal diffusivity. A Prandtl number of unity indicates that momentum and thermal diffusivity are comparable, and velocity and thermal boundary layers almost coincide with each other. If the Prandtl number is less than 1, which is the case for air at standard conditions, the thermal boundary layer is thicker than the velocity boundary layer. If the Prandtl number is greater than 1, the thermal boundary layer is thinner than the velocity boundary layer. Air at room temperature has a Prandtl number of 0.71, and for water, at 18°C, it is around 7.56, which means that the thermal diffusivity is more dominant for air than for water.
Similarly, as for Prandtl Number, the Lewis number physically relates the relative thickness of the thermal layer and mass-transfer (concentration) boundary layer. The Schmidt number physically relates the relative thickness of the velocity boundary layer and mass-transfer (concentration) boundary layer.
where n = 1/3 for most applications in all three relations. These relations, in general, are applicable only for laminar flow and are not applicable to turbulent boundary layers since turbulent mixing, in this case, may dominate the diffusion processes.
Heat transfer by convection is more difficult to analyze than heat transfer by conduction because no single property of the heat transfer medium, such as thermal conductivity, can be defined to describe the mechanism. Convective heat transfer is complicated by the fact that it involves fluid motion as well as heat conduction. Heat transfer by convection varies from situation to situation (upon the fluid flow conditions), and it is frequently coupled with the mode of fluid flow. In forced convection, the rate of heat transfer through a fluid is much higher by convection than by conduction.
In practice, analysis of heat transfer by convection is treated empirically (by direct experimental observation). Most problems can be solved using so-called characteristic numbers (e.g., Nusselt number). Characteristic numbers are dimensionless numbers used to describe a character of heat transfer. They can be used to compare a real situation (e.g., heat transfer in a pipe) with a small-scale model. Experience shows that convection heat transfer strongly depends on the fluid properties, dynamic viscosity, thermal conductivity, density, and specific heat, as well as the fluid velocity. It also depends on the geometry and the roughness of the solid surface, and the type of fluid flow. All these conditions affect especially the stagnant film thickness.
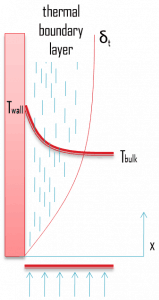
Convection involves the transfer of heat between a surface at a given temperature (Twall) and fluid at a bulk temperature (Tb). The exact definition of the bulk temperature (Tb) varies depending on the details of the situation.
- For flow adjacent to a hot or cold surface, Tb is the temperature of the fluid “far” from the surface.
- For boiling or condensation, Tb is the saturation temperature of the fluid.
- For flow in a pipe, Tb is the average temperature measured at a particular cross-section of the pipe.
Newton’s Law of Cooling for Convection
Despite the complexity of convection, the rate of convection heat transfer is observed to be proportional to the temperature difference. It is conveniently expressed by Newton’s law of cooling, which states that:
The rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its surroundings, provided the temperature difference is small, and the nature of radiating surface remains the same.
Note that ΔT is given by the surface or wall temperature, Twall, and the bulk temperature, T∞, which is the temperature of the fluid sufficiently far from the surface.
Convective Heat Transfer Coefficient
As can be seen, the constant of proportionality will be crucial in calculations, and it is known as the convective heat transfer coefficient, h. The convective heat transfer coefficient, h, can be defined as:
The rate of heat transfer between a solid surface and a fluid per unit surface area per unit temperature difference.
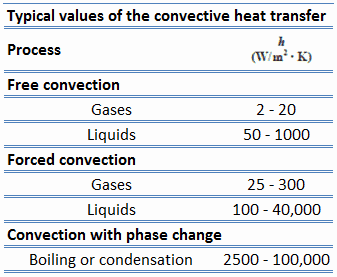The convective heat transfer coefficient depends on the fluid’s physical properties and the physical situation. The convective heat transfer coefficient is not a property of the fluid. It is an experimentally determined parameter whose value depends on all the variables influencing convection, such as the surface geometry, the nature of fluid motion, the properties of the fluid, and the bulk fluid velocity.
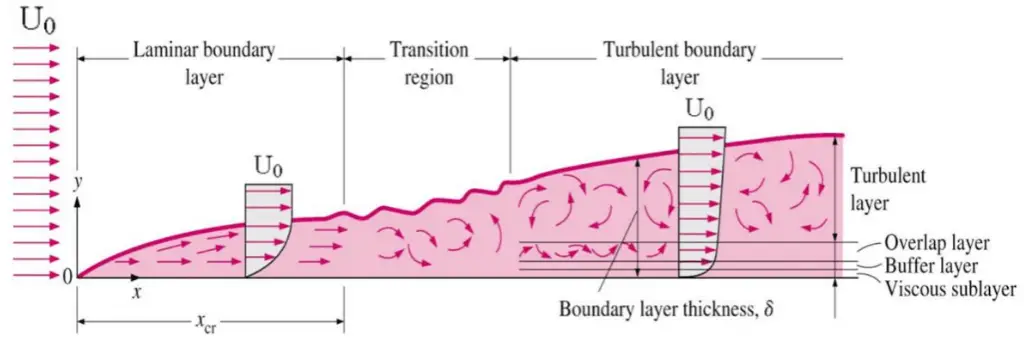
Typically, the convective heat transfer coefficient for laminar flow is relatively low compared to the convective heat transfer coefficient for turbulent flow. This is due to turbulent flow having a thinner stagnant fluid film layer on the heat transfer surface.
It must be noted this stagnant fluid film layer plays a crucial role in the convective heat transfer coefficient. It is observed that the fluid comes to a complete stop at the surface and assumes a zero velocity relative to the surface. This phenomenon is known as the no-slip condition, and therefore, at the surface, energy flow occurs purely by conduction. But in the next layers, both conduction and diffusion-mass movement occur at the molecular or macroscopic levels. Due to the mass movement, the rate of energy transfer is higher. As was written, nucleate boiling at the surface effectively disrupts this stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid.
A similar phenomenon occurs for the temperature. It is observed that the fluid’s temperature at the surface and the surface will have the same temperature at the point of contact. This phenomenon is known as the no-temperature-jump condition, and it is very important for the theory of nucleate boiling.
Values of the heat transfer coefficient, h, have been measured and tabulated for the commonly encountered fluids and flow situations occurring during heat transfer by convection.
Thermal resistance is a heat property and a measurement of a temperature difference by which an object or material resists a heat flow. The thermal resistance for conduction in a plane wall is defined as:
The equation above can also be derived for convective heat transfer. For heat flow is analogous to the relation for electric current flow I, expressed as:
where Re = L/σeA is the electric resistance and V1 – V2 is the voltage difference across the resistance (σe is the electrical conductivity). The analogy between both equations is obvious. The rate of heat transfer through a layer corresponds to the electric current, the thermal resistance corresponds to electrical resistance, and the temperature difference corresponds to the voltage difference across the layer. The temperature difference is the potential or driving function for the heat flow, resulting in the Fourier equation being written similarly to Ohm’s Law of Electrical Circuit Theory.
Circuit representations provide a useful tool for conceptualizing and quantifying heat transfer problems. This analogy can also be used for the thermal resistance of the surface against heat convection. Note that when the convection heat transfer coefficient is very large (h → infinity), the convection resistance becomes zero and the surface temperature approaches the bulk temperature. This situation is approached in practice at surfaces where intensive boiling and condensation occur.
The heat transfer through the composite wall can be calculated from these resistances. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.
The equivalent thermal circuit for the plane wall with convection surface conditions is shown in the figure.
See also: Wiedemann–Franz Law
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem. For example, heat transfer in a steam generator involves convection from the bulk of the reactor coolant to the steam generator inner tube surface, conduction through the tube wall, and convection (boiling) from the outer tube surface to the secondary side fluid.
In cases of combined heat transfer for a heat exchanger, there are two values for h. The convective heat transfer coefficient (h) for the fluid film inside the tubes and a convective heat transfer coefficient for the fluid film outside the tubes. The tube wall’s thermal conductivity (k) and thickness (Δx) must also be accounted for.
Overall Heat Transfer Coefficient – Plane Wall
Overall Heat Transfer Coefficient – Cylindrical Tubes
Steady heat transfer through multilayered cylindrical or spherical shells can be handled just like multilayered plane walls.
Nusselt Number
The Nusselt number is a dimensionless number, named after a German engineer Wilhelm Nusselt. The Nusselt number is closely related to the Péclet number. Both numbers are used to describe the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid. Nusselt number is equal to the dimensionless temperature gradient at the surface, and it provides a measure of the convection heat transfer occurring at the surface. The conductive component is measured under the same conditions as the heat convection but with stagnant fluid. The Nusselt number is to the thermal boundary layer what the friction coefficient is to the velocity boundary layer. Thus, the Nusselt number is defined as:
where:
kf is the thermal conductivity of the fluid [W/m.K]
L is the characteristic length
h is the convective heat transfer coefficient [W/m2.K]
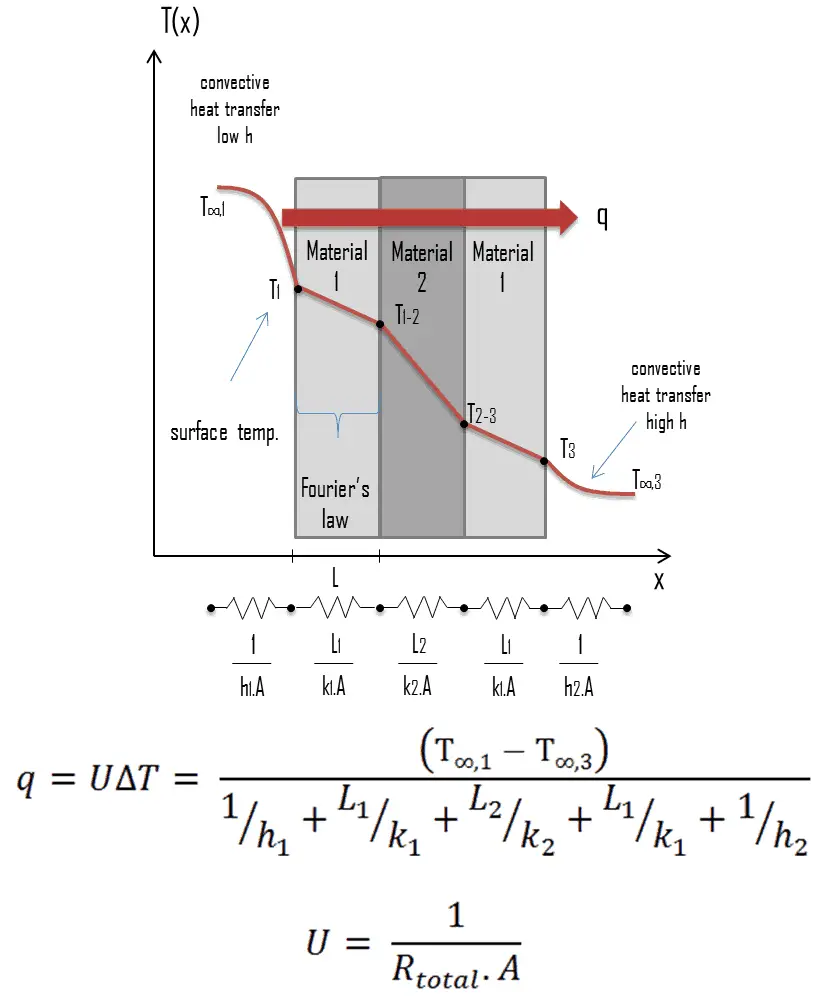
For illustration, consider a fluid layer of thickness L and temperature difference ΔT. Heat transfer through the fluid layer will be by convection when the fluid involves some motion and conduction when the fluid layer is motionless.
In the case of conduction, the heat flux can be calculated using Fourier’s law of conduction. In the case of convection, the heat flux can be calculated using Newton’s law of cooling. Taking their ratio gives:
The preceding equation defines the Nusselt number. Therefore, the Nusselt number represents the enhancement of heat transfer through a fluid layer due to convection relative to conduction across the same fluid layer. A Nusselt number of Nu=1 for a fluid layer represents heat transfer across the layer by pure conduction. The larger the Nusselt number, the more effective the convection. A larger Nusselt number corresponds to more effective convection, with turbulent flow typically in the 100–1000 range. The Nusselt number is usually a function of the Reynolds number and the Prandtl number for turbulent flow.
Example – Convective Heat Transfer – Cladding Surface Temperature
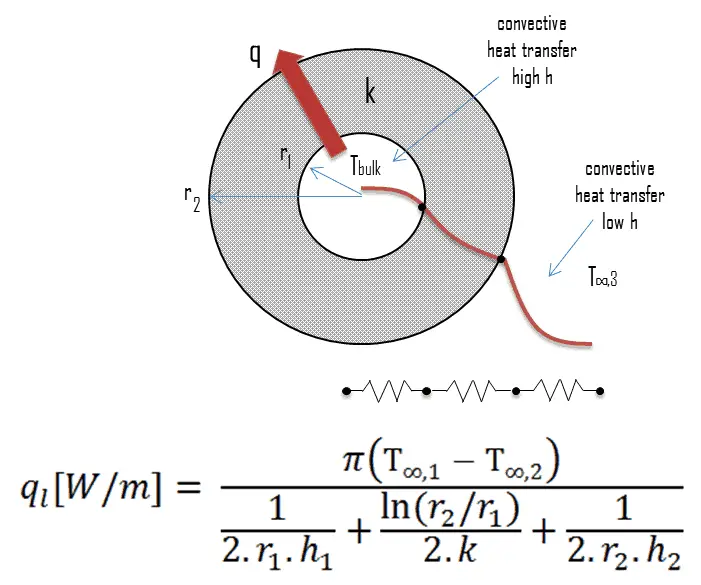
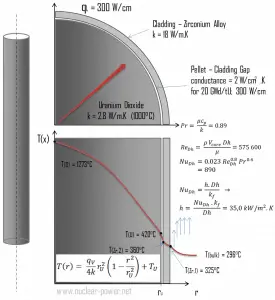Cladding is the outer layer of the fuel rods, standing between the reactor coolant and the nuclear fuel (i.e., fuel pellets). It is made of corrosion-resistant material with a low absorption cross-section for thermal neutrons, usually zirconium alloy. Cladding prevents radioactive fission products from escaping the fuel matrix into the reactor coolant and contaminating it. Cladding constitutes one of the barriers in the ‘defense-in-depth ‘approach; therefore, its coolability is one of the key safety aspects.
Consider the fuel cladding of inner radius rZr,2 = 0.408 cm and outer radius rZr,1 = 0.465 cm. Compared to fuel pellet, there is almost no heat generation in the fuel cladding (cladding is slightly heated by radiation). All heat generated in the fuel must be transferred via conduction through the cladding, and therefore the inner surface is hotter than the outer surface.
Assume that:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the pitch of fuel pins is: p = 13 mm
- the thermal conductivity of saturated water at 300°C is: kH2O = 0.545 W/m.K
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the fluid density is: ρ = 714 kg/m3
- the specific heat is: cp = 5.65 kJ/kg.K
- the core flow velocity is constant and equal to Vcore = 5 m/s
- the temperature of reactor coolant at this axial coordinate is: Tbulk = 296°C
- the linear heat rate of the fuel is qL = 300 W/cm (FQ ≈ 2.0) and thus the volumetric heat rate is qV = 597 x 106 W/m3
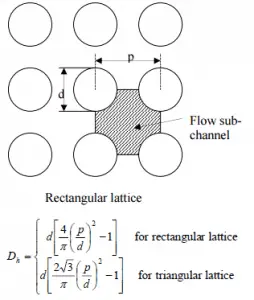Calculate the Prandtl, Reynolds and Nusselt number for this flow regime (internal forced turbulent flow) inside the rectangular fuel lattice (fuel channel), then calculate the heat transfer coefficient and finally the cladding surface temperature, TZr,1.
To calculate the cladding surface temperature, we have to calculate the Prandtl, Reynolds, and Nusselt number because the heat transfer for this flow regime can be described by the Dittus-Boelter equation, which is:
Calculation of the Prandtl number
To calculate the Prandtl number, we have to know:
- the thermal conductivity of saturated water at 300°C is: kH2O = 0.545 W/m.K
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the specific heat is: cp = 5.65 kJ/kg.K
Note that all these parameters significantly differ for water at 300°C from those at 20°C. Prandtl number for water at 20°C is around 6.91. Prandtl number for reactor coolant at 300°C is then:
Calculation of the Reynolds number
To calculate the Reynolds number, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm (to calculate the hydraulic diameter)
- the pitch of fuel pins is: p = 13 mm (to calculate the hydraulic diameter)
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the fluid density is: ρ = 714 kg/m3
The hydraulic diameter, Dh, is a commonly used term when handling flow in non-circular tubes and channels. The hydraulic diameter of the fuel channel, Dh, is equal to 13,85 mm.
See also: Hydraulic Diameter
The Reynolds number inside the fuel channel is then equal to:
This fully satisfies the turbulent conditions.
Calculation of the Nusselt number using Dittus-Boelter equation
For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known DittusBoelter equation.
To calculate the Nusselt number, we have to know:
- the Reynolds number, which is ReDh = 575600
- the Prandtl number, which is Pr = 0.89
The Nusselt number for the forced convection inside the fuel channel is then equal to:
Calculation of the heat transfer coefficient and the cladding surface temperature, TZr,1
Detailed knowledge of geometry, fluid parameters, the outer radius of cladding, linear heat rate, convective heat transfer coefficient allows us to calculate the temperature difference ∆T between the coolant (Tbulk) and the cladding surface (TZr,1).
To calculate the cladding surface temperature, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the Nusselt number, which is NuDh = 890
- the hydraulic diameter of the fuel channel is Dh = 13,85 mm
- the thermal conductivity of reactor coolant (300°C) is: kH2O = 0.545 W/m.K
- the bulk temperature of reactor coolant at this axial coordinate is Tbulk = 296°C
- the linear heat rate of the fuel is: qL = 300 W/cm (FQ ≈ 2.0)
The convective heat transfer coefficient, h, is given directly by the definition of Nusselt number:
Finally, we can calculate the cladding surface temperature (TZr,1) simply using Newton’s Law of Cooling:
For PWRs at normal operation, there is compressed liquid water inside the reactor core, loops, and steam generators. The pressure is maintained at approximately 16MPa. At this pressure, water boils at approximately 350°C(662°F). As can be seen, the surface temperature TZr,1 = 325°C ensures that even subcooled boiling does not occur. Note that subcooled boiling requires TZr,1 = Tsat. Since the inlet temperatures of the water are usually about 290°C (554°F), it is obvious this example corresponds to the lower part of the core. At higher core elevations, the bulk temperature may reach up to 330°C. The temperature difference of 29°C causes the subcooled boiling may occur (330°C + 29°C > 350°C). On the other hand, nucleate boiling at the surface effectively disrupts the stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid. As a result, the convective heat transfer coefficient significantly increases, and therefore at higher elevations, the temperature difference (TZr,1 – Tbulk) significantly decreases.