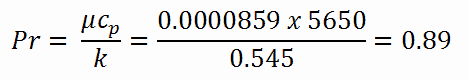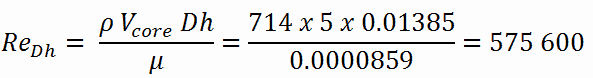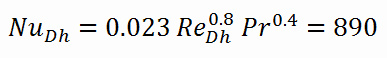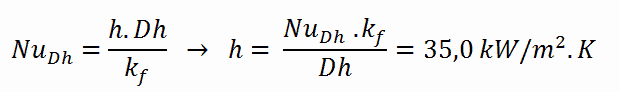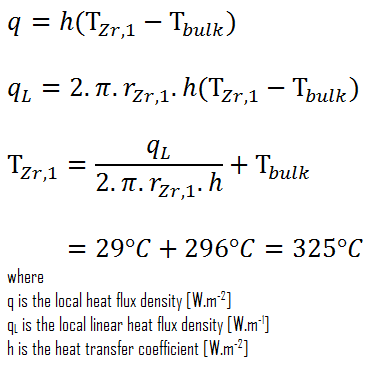Dittus-Boelter Equation

Sieder-Tate Equation

When the difference between the surface and the fluid temperatures is large, it may be necessary to account for the viscosity variation with temperature. Therefore a modified form of the Dittus-Boelter equation was proposed by Sieder and Tate (1936).

Gnielinski Equation

Although the Dittus-Boelter and Sieder-Tate equations are easily applied and are certainly satisfied for the purposes of this article, errors as large as 25% may result from their use. Such errors may be reduced by using more recent but generally more complex correlations such as the Gnielinski correlation. This equation validates tubes over a large Reynolds number range, including the transition region.

The Darcy friction factor, f, is a dimensionless quantity used in the Darcy–Weisbach equation for the description of frictional losses in pipe or duct as well as for open-channel flow. This is also called the Darcy–Weisbach friction factor, resistance coefficient, or simply friction factor.

Rough-walled Tubes

We also note that all these equations pertain to smooth tubes. The heat transfer coefficient increases with wall roughness for turbulent flow in rough tubes. As the Reynolds number increases, the viscous sublayer becomes thinner and smaller. The viscous sublayer becomes so thin that the surface roughness protrudes into the flow at a very high Reynolds number. The frictional losses, in this case, are produced in the main flow primarily by the protruding roughness elements, and the contribution of the laminar sublayer is negligible.

Special Reference: A Heat Transfer Textbook,  John H. Lienhard IV and John H. Lienhard V. Phlogiston Press, 2012.

Example – Dittus-Boelter Equation – Cladding Surface Temperature

Cladding is the outer layer of the fuel rods, standing between the reactor coolant and the nuclear fuel (i.e., fuel pellets). It is made of corrosion-resistant material with a low absorption cross-section for thermal neutrons, usually zirconium alloy. Cladding prevents radioactive fission products from escaping the fuel matrix into the reactor coolant and contaminating it. Cladding constitutes one of the barriers in the ‘defense-in-depth ‘ approach; therefore, its coolability is one of the key safety aspects.

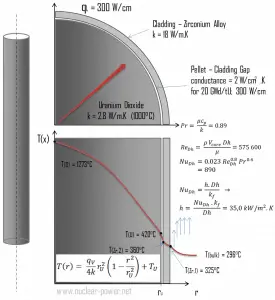
Consider the fuel cladding of inner radius r_Zr,2 = 0.408 cm and outer radius r_Zr,1 = 0.465 cm. Compared to fuel pellet, there is almost no heat generation in the fuel cladding (cladding is slightly heated by radiation). All heat generated in the fuel must be transferred via conduction through the cladding, and therefore the inner surface is hotter than the outer surface.

Assume that:

• the outer diameter of the cladding is: d = 2 x r_Zr,1 = 9,3 mm
• the pitch of fuel pins is: p = 13 mm
• the thermal conductivity of saturated water at 300°C is: k_H2O = 0.545 W/m.K
• the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m²
• the fluid density is: ρ = 714 kg/m³
• the specific heat is: c_p = 5.65 kJ/kg.K
• the core flow velocity is constant and equal to V_core = 5 m/s
• the temperature of reactor coolant at this axial coordinate is: T_bulk = 296°C
• the linear heat rate of the fuel is q_L = 300 W/cm (F_Q ≈ 2.0) and thus the volumetric heat rate is q_V = 597 x 10⁶ W/m³

Calculate the Prandtl, Reynolds and Nusselt number for this flow regime (internal forced turbulent flow) inside the rectangular fuel lattice (fuel channel), then calculate the heat transfer coefficient and finally the cladding surface temperature, T_Zr,1.

To calculate the cladding surface temperature, we have to calculate the Prandtl, Reynolds, and Nusselt number because the heat transfer for this flow regime can be described by the Dittus-Boelter equation, which is:

Calculation of the Prandtl number

To calculate the Prandtl number, we have to know:

• the thermal conductivity of saturated water at 300°C is: k_H2O = 0.545 W/m.K
• the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m²
• the specific heat is: c_p = 5.65 kJ/kg.K

Note that all these parameters significantly differ for water at 300°C from those at 20°C. Prandtl number for water at 20°C is around 6.91. Prandtl number for reactor coolant at 300°C is then:

Calculation of the Reynolds number

To calculate the Reynolds number, we have to know:

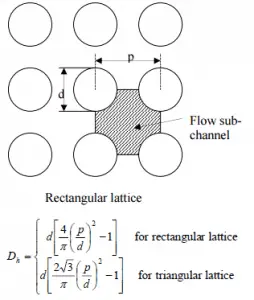
• the outer diameter of the cladding is: d = 2 x r_Zr,1 = 9,3 mm (to calculate the hydraulic diameter)
• the pitch of fuel pins is: p = 13 mm  (to calculate the hydraulic diameter)
• the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m²
• the fluid density is: ρ = 714 kg/m³

The hydraulic diameter, D_h, is a commonly used term when handling flow in non-circular tubes and channels. The hydraulic diameter of the fuel channel, D_h, is equal to 13,85 mm.

See also: Hydraulic Diameter

The Reynolds number inside the fuel channel is then equal to:

This fully satisfies the turbulent conditions.

Calculation of the Nusselt number using Dittus-Boelter equation

For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus–Boelter equation.

To calculate the Nusselt number, we have to know:

• the Reynolds number, which is Re_Dh = 575600
• the Prandtl number, which is Pr = 0.89

The Nusselt number for the forced convection inside the fuel channel is then equal to:

Calculation of the heat transfer coefficient and the cladding surface temperature, T_Zr,1

Detailed knowledge of geometry, fluid parameters, the outer radius of cladding, linear heat rate, convective heat transfer coefficient allows us to calculate the temperature difference ∆T between the coolant (T_bulk) and the cladding surface (T_Zr,1).

To calculate the cladding surface temperature, we have to know:

• the outer diameter of the cladding is: d = 2 x r_Zr,1 = 9,3 mm
• the Nusselt number, which is Nu_Dh = 890
• the hydraulic diameter of the fuel channel is D_h = 13,85 mm
• the thermal conductivity of reactor coolant (300°C) is: k_H2O = 0.545 W/m.K
• the bulk temperature of reactor coolant at this axial coordinate is T_bulk = 296°C
• the linear heat rate of the fuel is: q_L = 300 W/cm (F_Q ≈ 2.0)

The convective heat transfer coefficient, h, is given directly by the definition of Nusselt number:

Finally, we can calculate the cladding surface temperature (T_Zr,1) simply using Newton’s Law of Cooling:

For PWRs at normal operation, there is compressed liquid water inside the reactor core, loops, and steam generators. The pressure is maintained at approximately 16MPa. At this pressure, water boils at approximately 350°C(662°F). As can be seen, the surface temperature T_Zr,1 = 325°C ensures that even subcooled boiling does not occur. Note that subcooled boiling requires T_Zr,1 = T_sat. Since the inlet temperatures of the water are usually about 290°C (554°F), it is obvious this example corresponds to the lower part of the core. At higher core elevations, the bulk temperature may reach up to 330°C. The temperature difference of 29°C causes the subcooled boiling may occur (330°C + 29°C > 350°C). On the other hand, nucleate boiling at the surface effectively disrupts the stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid. As a result, the convective heat transfer coefficient significantly increases, and therefore at higher elevations, the temperature difference (T_Zr,1 – T_bulk) significantly decreases.