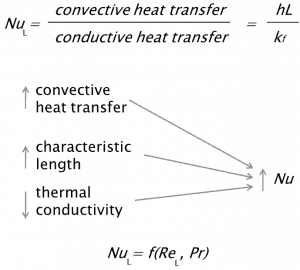
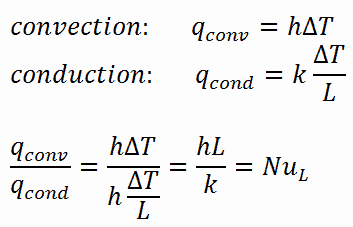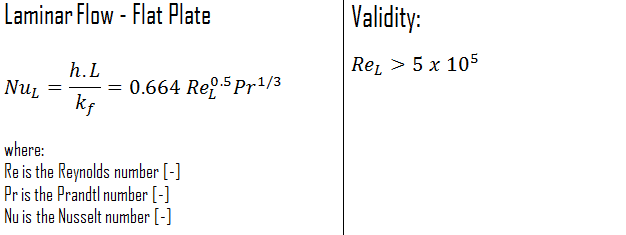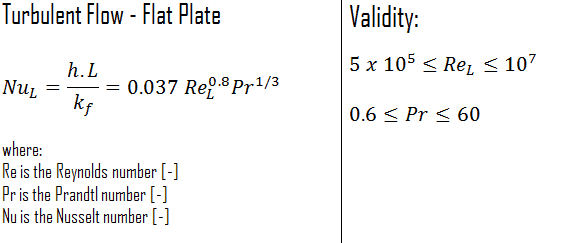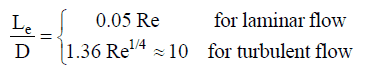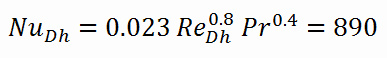Facebook Instagram Youtube Twitter

External vs. Internal – Nusselt Number

The flow regime can be also classified according to the geometry of a conduit or flow area. From this point of view, we distinguish:

Internal flow is a flow for which the fluid is confined by a surface. Detailed knowledge of the behavior of internal flow regimes is important in engineering because circular pipes can withstand high pressures and hence are used to convey liquids. On the other hand, external flow is such a flow in which boundary layers develop freely, without constraints imposed by adjacent surfaces. Detailed knowledge of the behavior of external flow regimes is important, especially in aeronautics and aerodynamics.

 
Nusselt Number
The Nusselt number is a dimensionless number, named after a German engineer Wilhelm Nusselt. The Nusselt number is closely related to the Péclet number. Both numbers are used to describe the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid. Nusselt number is equal to the dimensionless temperature gradient at the surface, and it provides a measure of the convection heat transfer occurring at the surface. The conductive component is measured under the same conditions as the heat convection but with stagnant fluid. The Nusselt number is to the thermal boundary layer what the friction coefficient is to the velocity boundary layer. Thus, the Nusselt number is defined as:

Nusselt Number - definition

where:

kf is the thermal conductivity of the fluid [W/m.K]

L is the characteristic length

h is the convective heat transfer coefficient [W/m2.K]

For illustration, consider a fluid layer of thickness L and temperature difference ΔT. Heat transfer through the fluid layer will be by convection when the fluid involves some motion and conduction when the fluid layer is motionless.

In the case of conduction, the heat flux can be calculated using Fourier’s law of conduction. In the case of convection, the heat flux can be calculated using Newton’s law of cooling. Taking their ratio gives:

nusselt number - convection to conduction

The preceding equation defines the Nusselt number. Therefore, the Nusselt number represents the enhancement of heat transfer through a fluid layer due to convection relative to conduction across the same fluid layer. A Nusselt number of Nu=1 for a fluid layer represents heat transfer across the layer by pure conduction. The larger the Nusselt number, the more effective the convection. A larger Nusselt number corresponds to more effective convection, with turbulent flow typically in the 100–1000 range. For turbulent flow, the Nusselt number is usually a function of the Reynolds number and the Prandtl number.

External Flow

In fluid dynamics, external flow is a flow in which boundary layers develop freely, without constraints imposed by adjacent surfaces. In comparison to internal flow, external flows feature highly viscous effects confined to rapidly growing “boundary layers” in the entrance region or thin shear layers along the solid surface. Accordingly, there will always exist a region of the flow outside the boundary layer. In this region, velocity, temperature, and/or concentration do not change, and their gradients may be neglected.

This effect causes the boundary layer to be expanding, and the boundary-layer thickness relates to the fluid’s kinematic viscosity.

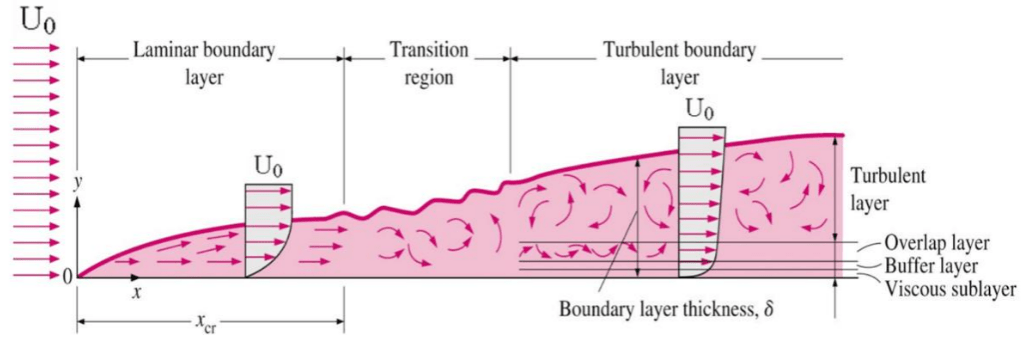
This is demonstrated in the following picture. Far from the body, the flow is nearly inviscid, and it can be defined as the flow of a fluid around a body that is completely submerged in it.

Boundary layer on flat plate

External Flow – Flat Plate

The average Nusselt number over the entire plate is determined by:

laminar flow - flat plate - nusselt number

This relation gives the average heat transfer coefficient for the entire plate when the flow is laminar over the entire plate.

turbulent flow - flat plate - nusselt number

This relation gives the average heat transfer coefficient for the entire plate only when the flow is turbulent over the entire plate, or when the laminar flow region of the plate is too small relative to the turbulent flow region.

Internal Flow

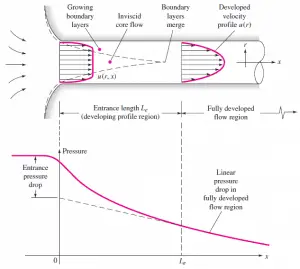
Internal Flow
Source: White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

In fluid dynamics, internal flow is a flow for which the fluid is confined by a surface. Detailed knowledge of the behavior of internal flow regimes is important in engineering because circular pipes can withstand high pressures and hence are used to convey liquids. Non-circular ducts are used to transport low-pressure gases, such as air in cooling and heating systems. The internal flow configuration is a convenient geometry for heating and cooling fluids used in energy conversion technologies such as nuclear power plants.

An entrance region is typical for the internal flow regime, and a nearly inviscid upstream flow converges and enters the tube in this region. To characterize this region, the hydrodynamic entrance length is introduced and is approximately equal to:

hydrodynamic entrance length

The maximum hydrodynamic entrance length, at ReD,crit = 2300 (laminar flow), is Le = 138d, where D is the diameter of the pipe. This is the longest development length possible. The boundary layers grow faster in turbulent flow, and Le is relatively shorter. For any given problem, Le / D has to be checked to see if Le is negligible compared to the pipe length. The entrance effects may be neglected at a finite distance from the entrance because the boundary layers merge and the inviscid core disappears. The tube flow is then fully developed.

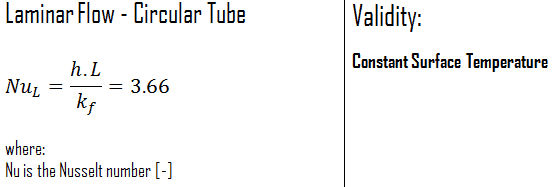
Internal Laminar Flow – Nusselt Number

Constant Surface Temperature

In laminar flow in a tube with constant surface temperature, both the friction factor and the heat transfer coefficient remain constant in the fully developed region.

Laminar Flow - Circular Tube - temperature

Constant Surface Heat Flux

Therefore, for fully developed laminar flow in a circular tube subjected to constant surface heat flux, the Nusselt number is a constant. There is no dependence on the Reynolds or the Prandtl numbers.

Laminar Flow - Circular Tube - flux

Internal Turbulent Flow – Nusselt Number

See also: Dittus-Boelter Equation

For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus-Boelter equation. The Dittus–Boelter equation is easy to solve. Still, it is less accurate when there is a large temperature difference across the fluid and is less accurate for rough tubes (many commercial applications) since it is tailored to smooth tubes.

Dittus-Boelter Equation - Formula

The Dittus-Boelter correlation may be used for small to moderate temperature differences, Twall – Tavg, with all properties evaluated at an, averaged temperature Tavg.

For flows characterized by large property variations, the corrections (e.g., a viscosity correction factor μ/μwall) must be taken into account, for example, as Sieder and Tate recommend.

Calculation of the Nusselt number using Dittus-Boelter equation

For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus–Boelter equation.

To calculate the Nusselt number, we have to know:

The Nusselt number for the forced convection inside the fuel channel is then equal to:

nusselt number - example

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Convection