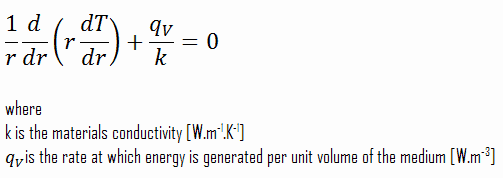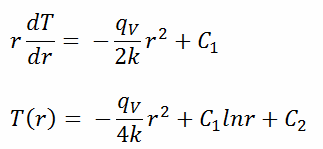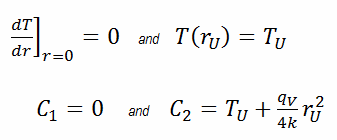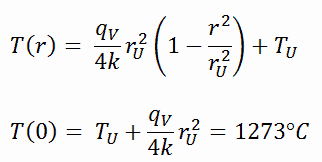Most PWRs use uranium fuel, which is in the form of uranium dioxide. Uranium dioxide is a black semiconducting solid with very low thermal conductivity. On the other hand, uranium dioxide has a very high melting point and has well-known behavior. The UO2 is pressed into cylindrical pellets, and these pellets are then sintered into the solid.
 These cylindrical pellets are then loaded and encapsulated within a fuel rod (or fuel pin) made of zirconium alloys due to their very low absorption cross-section (unlike stainless steel). The surface of the tube, which covers the pellets, is called fuel cladding.
These cylindrical pellets are then loaded and encapsulated within a fuel rod (or fuel pin) made of zirconium alloys due to their very low absorption cross-section (unlike stainless steel). The surface of the tube, which covers the pellets, is called fuel cladding.
See also: Thermal Conduction of Uranium Dioxide
The thermal and mechanical behavior of fuel pellets and fuel rods constitute one of three key core design disciplines. Nuclear fuel is operated under inhospitable conditions (thermal, radiation, mechanical) and must withstand more than normal conditions operation. For example, temperatures in the center of fuel pellets reach more than 1000°C (1832°F), accompanied by fission-gas releases. Therefore detailed knowledge of temperature distribution within a single fuel rod is essential for the safe operation of nuclear fuel. This section will study the heat conduction equation in cylindrical coordinates using Dirichlet boundary conditions with given surface temperature (i.e., using Dirichlet boundary condition). Comprehensive analysis of fuel rod temperature profile will be studied separately.
See also: Heat Generation in Nuclear Reactors
See also: Cladding Surface Temperature
The temperature in the centerline of a fuel pellet
Consider the fuel pellet of radius rU = 0.40 cm, in which there is uniform and constant heat generation per unit volume, qV [W/m3]. Instead of volumetric heat rate qV [W/m3], engineers often use the linear heat rate, qL [W/m], representing the heat rate of one meter of a fuel rod. The linear heat rate can be calculated from the volumetric heat rate by:
The centreline is taken as the origin for r-coordinate. Due to symmetry in the z-direction and azimuthal direction, we can separate variables and simplify this problem to a one-dimensional problem. Thus, we will only solve for the temperature as a function of radius, T(r). For constant thermal conductivity, k, the appropriate form of the cylindrical heat equation, is:
The general solution of this equation is:
where C1 and C2 are the constants of integration.
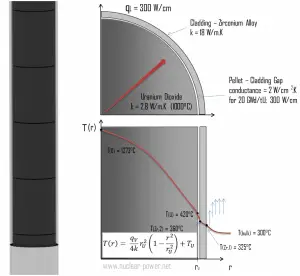
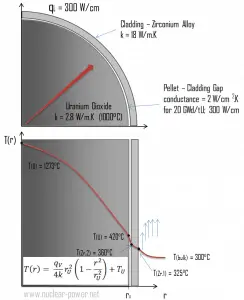 Calculate the temperature distribution, T(r), in this fuel pellet, if:
Calculate the temperature distribution, T(r), in this fuel pellet, if:
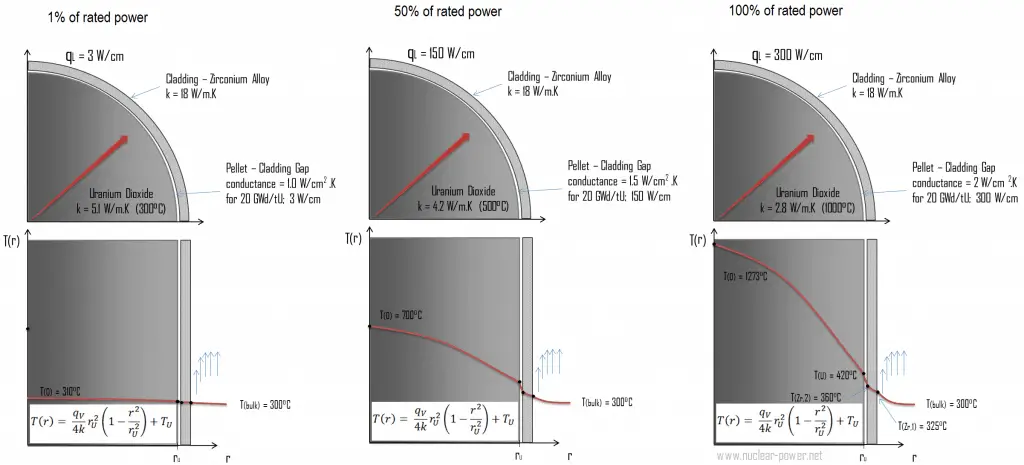
- the temperature at the surface of the fuel pellet is TU = 420°C
- the fuel pellet radius rU = 4 mm.
- the averaged material’s conductivity is k = 2.8 W/m.K (corresponds to uranium dioxide at 1000°C)
- the linear heat rate is qL = 300 W/cm and thus the volumetric heat rate is qV = 597 x 106 W/m3
In this case, the surface is maintained at given temperatures TU. This corresponds to the Dirichlet boundary condition. Moreover, this problem is thermally symmetric, and therefore we may also use thermal symmetry boundary conditions. The constants may be evaluated using substitution into the general solution and are of the form:
The resulting temperature distribution and the centerline (r = 0) temperature (maximum) in this cylindrical fuel pellet at these specific boundary conditions will be:
The radial heat flux at any radius, qr [W.m-1], in the cylinder may, of course, be determined by using the temperature distribution and with Fourier’s law. Note that, with heat generation, the heat flux is no longer independent of r.
The following figure shows the temperature distribution in the fuel pellet at various power levels.
______
The temperature in an operating reactor varies from point to point within the system. Consequently, there is always one fuel rod and one local volume hotter than all the rest. The peak power limits must be introduced to limit these hot places. The peak power limits are associated with a boiling crisis and conditions that could cause fuel pellet melt. However, metallurgical considerations place upper limits on the temperature of the fuel cladding and the fuel pellet. Above these temperatures, there is a danger that the fuel may be damaged. One of the major objectives in the design of nuclear reactors is to remove the heat produced at the desired power level while assuring that the maximum fuel temperature and the maximum cladding temperature are always below these predetermined values.
See also: Cladding Surface Temperature