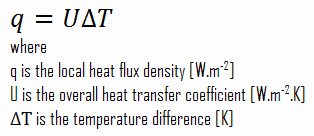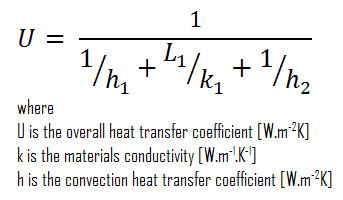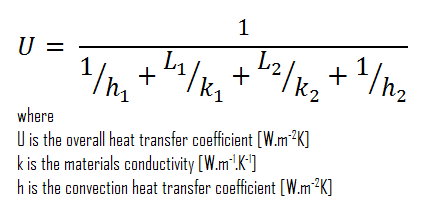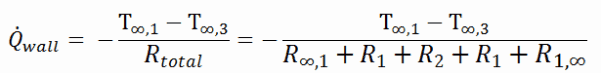Heat losses from hotter objects occur by three mechanisms (either individually or in combination):
- Heat Conduction. Heat conduction, also called diffusion, occurs within a body or between two bodies in contact. It is the direct microscopic exchange of kinetic energy of particles through the boundary between two systems. When an object is at a different temperature from another body or its surroundings
- Heat Convection. Heat convection depends on the motion of mass from one region of space to another. Heat convection occurs when the bulk flow of a fluid (gas or liquid) carries heat along with the flow of matter in the fluid.
- Thermal Radiation. Radiation is heat transfer by electromagnetic radiation, such as sunshine, with no need for the matter to be present in the space between bodies.
Thermal insulators have very low thermal conductivity. Their low thermal conductivity is based on the alternation of gas pocket and solid material that causes the heat must be transferred through many interfaces causing a rapid decrease in heat transfer coefficient.
As was written, many heat transfer processes involve composite systems and even involve a combination of conduction and convection. It is often convenient to work with an overall heat transfer coefficient, known as a U-factor with these composite systems.
While thermal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing spontaneously from one body to another due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level due to a temperature difference. When a temperature difference does exist, heat flows spontaneously from the warmer system to the colder system, never the reverse. This direction of thermodynamic processes is given by the second law of thermodynamics.
As a result, any object hotter than the surroundings must continuously lose a part of its thermal energy. This is a natural behavior of all objects. When the flow of heat stops, they are said to be at the same temperature, and they are then said to be in thermal equilibrium. Heat losses from hotter objects occur by three mechanisms (either individually or in combination):
- Heat Conduction. Heat conduction, also called diffusion, occurs within a body or between two bodies in contact. It is the direct microscopic exchange of kinetic energy of particles through the boundary between two systems. When an object is at a different temperature from another body or its surroundings
- Heat Convection. Heat convection depends on the mass movement from one region of space to another. Heat convection occurs when the bulk flow of a fluid (gas or liquid) carries heat along with the flow of matter in the fluid.
- Thermal Radiation. Radiation is heat transfer by electromagnetic radiation, such as sunshine, with no need for the matter to be present in the space between bodies.
Heat Losses – Clothing
The purpose of clothing is similar. The insulating properties of clothing come from the insulating properties of air. Gases possess poor thermal conduction properties compared to liquids and solids and thus make a good insulation material if they can be trapped (e.g., in a foam-like structure). Air and other gases are generally good insulators. But the main benefit is in the absence of convection. Without clothes, our bodies in still air would heat the air in direct contact with the skin and soon become reasonably comfortable because air is a very good insulator. It must be added. Also, in this case, air will be flowing due to natural convection. In natural convection, the air surrounding a body receives heat and, by thermal expansion, becomes less dense and rises. Thermal expansion of air plays a crucial role. In other words, heavier (more dense) components will fall while lighter (less dense) components rise, leading to bulk air movement.
In the wind, the warm air surrounding our body would be replaced by cold air, thus increasing the temperature difference and the heat loss from the body. Clothes constitute a barrier to this moving air, and the main benefit is in the absence of large-scale convection. Moreover, clothes are made from materials that are generally good insulators. Many insulating materials (e.g., wool) function simply by having many gas-filled pockets, which significantly decrease the material’s thermal conductivity. Alternation of gas pocket and solid material causes heat to transfer through many interfaces, causing a rapid decrease in heat transfer coefficient.
Heat Losses – Thermal Insulation
To minimize heat losses in industry and also in the construction of buildings, thermal insulation is widely used. The purpose of thermal insulation is to reduce the overall heat transfer coefficient by adding material with low thermal conductivity. Thermal insulation in buildings is an important factor in achieving thermal comfort for occupants. Thermal insulation reduces unwanted heat loss and also reduces unwanted heat gain. Therefore thermal insulation can decrease the energy demands of heating and cooling systems. It must be added that no material can completely prevent heat losses, and heat losses can only be minimized.
Similarly, as for clothing, thermal insulation is based on low thermal conductivity materials and geometry (e.g., double-pane windows). The insulating properties of these materials come from the insulating properties of air. Many insulating materials (e.g., glass wool) function simply by having a large number of gas-filled pockets which prevent large-scale convection. The geometry of these materials also plays a crucial role. For example, increasing the width of the air layer, such as using two panes of glass separated by an air gap, will reduce the heat loss more than simply increasing the glass thickness since the thermal conductivity of air is much less than that for glass.
Example – Heat Loss through a Wall
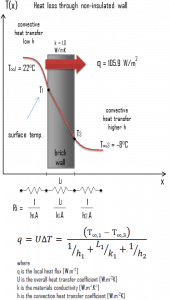A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend on ambient and interior conditions (wind, humidity, etc.).
- Calculate the heat flux (heat loss) through this non-insulated wall.
- Now assume thermal insulation on the outer side of this wall. Use expanded polystyrene insulation 10 cm thick (L2) with the thermal conductivity of k2 = 0.03 W/m.K and calculate the heat flux (heat loss) through this composite wall.
Solution:
As was written, many heat transfer processes involve composite systems and even involve a combination of conduction and convection. With these composite systems, it is often convenient to work with an overall heat transfer coefficient, known as a U-factor. The U-factor is defined by an expression analogous to Newton’s law of cooling:
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.
- bare wall
Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 1/30) = 3.53 W/m2K
The heat flux can be then calculated simply as:
q = 3.53 [W/m2K] x 30 [K] = 105.9 W/m2
The total heat loss through this wall will be:
qloss = q . A = 105.9 [W/m2] x 30 [m2] = 3177W
- composite wall with thermal insulation
Assuming one-dimensional heat transfer through the plane composite wall, no thermal contact resistance, and disregarding radiation, the overall heat transfer coefficient can be calculated as:
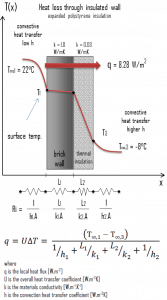The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 0.1/0.03 + 1/30) = 0.276 W/m2K
The heat flux can be then calculated simply as:
q = 0.276 [W/m2K] x 30 [K] = 8.28 W/m2
The total heat loss through this wall will be:
qloss = q . A = 8.28 [W/m2] x 30 [m2] = 248 W
As can be seen, adding a thermal insulator causes a significant decrease in heat losses. It must be added that adding the next layer of the thermal insulator does not cause such high savings. This can be better seen from the thermal resistance method, which can be used to calculate the heat transfer through composite walls. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.
Example – Heat Loss through a Window
Heat loss through windows
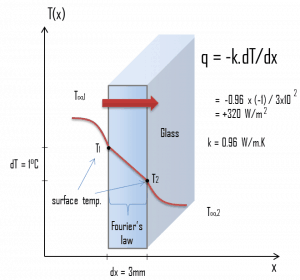
A major source of heat loss from a house is through the windows. Calculate the rate of heat flux through a glass window 1.5 m x 1.0 m in area and 3.0 mm thick if the temperatures at the inner and outer surfaces are 14.0°C and 13.0°C, respectively. Calculate the heat flux through this window.
Solution:
At this point, we know the temperatures on the surfaces of the material, and these temperatures are also given by conditions inside the house and outside the house. In this case, heat flows by conduction through the glass from the higher inside temperature to the lower outside temperature. We use the heat conduction equation:
We assume that the thermal conductivity of a common glass is k = 0.96 W/m.K.
The heat flux will then be:
q = 0.96 [W/m.K] x 1 [K] / 3.0 x 10-3 [m] = 320 W/m2
The total heat loss through this window will be:
qloss = q . A = 320 x 1.5 x 1.0 = 480W
It must be added that 15°C is not very warm for the living room of a house. But this temperature does not correspond to the interior temperature but corresponds to the surface temperature. Due to the finite convective heat transfer coefficient, there is always a considerable temperature drop between the interior and window surface temperatures. Note that both convection coefficients strongly depend on ambient and interior conditions (wind, humidity, etc.).
See also: Convective Heat Transfer Coefficient
Similarly, as for clothing, thermal insulation is based on low thermal conductivity materials and geometry (e.g., double-pane windows). The insulating properties of these materials come from the insulating properties of air. Many insulating materials (e.g., wool) function simply by having a large number of gas-filled pockets which prevent large-scale convection. The geometry of these materials also plays a crucial role. For example, increasing the width of the air layer, such as using two panes of glass separated by an air gap, will reduce the heat loss more than simply increasing the glass thickness since the thermal conductivity of air is much less than that for glass.
