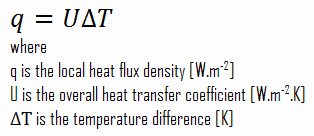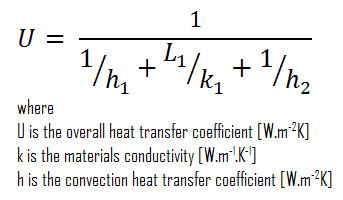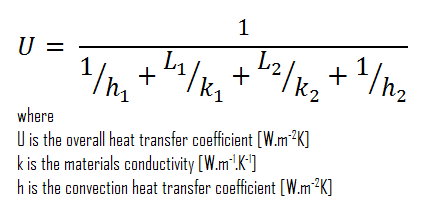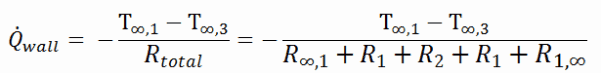The purpose of thermal insulation is to reduce the overall heat transfer coefficient by adding materials with low thermal conductivity.
Thermal insulation in buildings is an important factor in achieving thermal comfort for occupants. Thermal insulation reduces unwanted heat loss and also reduces unwanted heat gain. Therefore thermal insulation can decrease the energy demands of heating and cooling systems. It must be added that no material can completely prevent heat losses. Heat losses can only be minimized.
 Similarly, as for clothing, thermal insulation is based on low thermal conductivity materials and geometry (e.g., double-pane windows). The insulating properties of these materials come from the insulating properties of air. Many insulating materials (e.g., wool) function simply by having a large number of gas-filled pockets which prevent large-scale convection. The geometry of these materials also plays a crucial role. For example, increasing the width of the air layer, such as using two panes of glass separated by an air gap, will reduce the heat loss more than simply increasing the glass thickness since the thermal conductivity of air is much less than that for glass.
Similarly, as for clothing, thermal insulation is based on low thermal conductivity materials and geometry (e.g., double-pane windows). The insulating properties of these materials come from the insulating properties of air. Many insulating materials (e.g., wool) function simply by having a large number of gas-filled pockets which prevent large-scale convection. The geometry of these materials also plays a crucial role. For example, increasing the width of the air layer, such as using two panes of glass separated by an air gap, will reduce the heat loss more than simply increasing the glass thickness since the thermal conductivity of air is much less than that for glass.
Insulation Materials
 As was written, thermal insulation is based on the use of substances with very low thermal conductivity. These materials are known as insulation materials. Common insulation materials are wool, fiberglass, rock wool, polystyrene, polyurethane, goose feather, etc. Therefore, these materials are very poor conductors of heat and are good thermal insulators.
As was written, thermal insulation is based on the use of substances with very low thermal conductivity. These materials are known as insulation materials. Common insulation materials are wool, fiberglass, rock wool, polystyrene, polyurethane, goose feather, etc. Therefore, these materials are very poor conductors of heat and are good thermal insulators.
It must be added that thermal insulation is primarily based on gases’ very low thermal conductivity. Gases possess poor thermal conduction properties compared to liquids and solids and thus make a good insulation material if they can be trapped (e.g., in a foam-like structure). Air and other gases are generally good insulators. But the main benefit is in the absence of convection. Therefore, many insulation materials (e.g., polystyrene) function simply by having many gas-filled pockets, which prevent large-scale convection. In all types of thermal insulation, evacuation of the air in the void space will further reduce the overall thermal conductivity of the insulator.
Alternation of gas pocket and solid material causes heat to transfer through many interfaces, causing a rapid decrease in heat transfer coefficient.
It must be noted, heat losses from hotter objects occur by three mechanisms (either individually or in combination):
So far, we have not discussed thermal radiation as a mode of heat loss. Radiation heat transfer is mediated by electromagnetic radiation, and therefore it does not require any medium for heat transfer. Energy transfer by radiation is fastest (at the speed of light), and it suffers no attenuation in a vacuum. Any material with a temperature above absolute zero gives off some radiant energy. Most energy of this type is in the infra-red region of the electromagnetic spectrum, although some of it is in the visible region. Materials with low emissivity (high reflectivity) should be used to decrease this type of heat transfer. Reflective insulations are usually composed of multilayered, parallel foils of high reflectivity, spaced to reflect thermal radiation to their source. The emissivity, ε, of the surface of a material is its effectiveness in emitting energy as thermal radiation and varies between 0.0 and 1.0. In general, polished metals have very low emissivity and therefore are widely used to reflect radiant energy to its source, as in the case of first aid blankets.
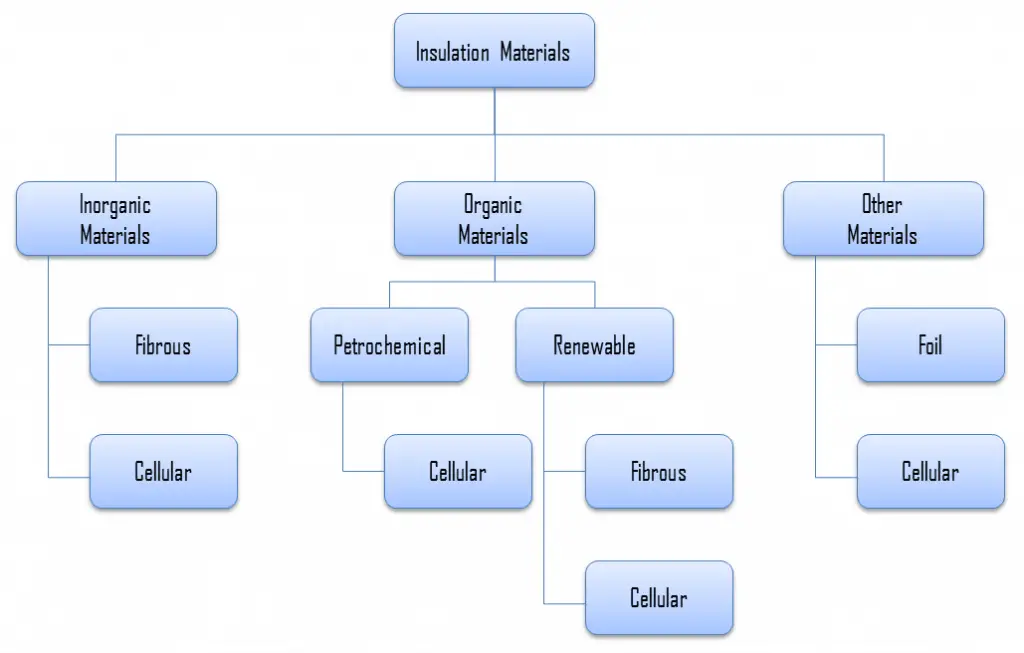
Types of Insulation – Categorization of Insulation Materials
For insulation materials, three general categories can be defined. These categories are based on the chemical composition of the base material from which the insulating material is produced.
In further reading, there is a brief description of these types of insulation materials.
Inorganic Insulation Materials
As can be seen from the figure, inorganic materials can be classified accordingly:
- Fibrous materials
- Glass wool
- Rock wool
- Cellular materials
- Calcium silicate
- Cellular glass
Organic Insulation Materials
The organic insulation materials treated in this section are all derived from a petrochemical or renewable feedstock (bio-based). Almost all of the petrochemical insulation materials are in the form of polymers. As can be seen from the figure, all petrochemical insulation materials are cellular. A material is cellular when the material’s structure consists of pores or cells. On the other hand, many plants contain fibers for their strength. Therefore almost all the bio-based insulation materials are fibrous (except expanded cork, which is cellular).
Organic insulation materials can be classified accordingly:
- Petrochemical materials (oil/coal-derived)
- Expanded polystyrene (EPS)
- Extruded polystyrene (XPS)
- Polyurethane (PUR)
- Phenolic foam
- Polyisocyanurate foam (PIR)
- Renewable materials (plant/animal-derived)
- Cellulose
- Cork
- Woodfibre
- Hemp fiber
- Flax wool
- Sheep’s wool
- Cotton insulation
Example – Heat Loss through a Wall
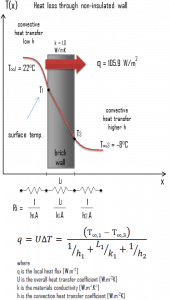 A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend on ambient and interior conditions (wind, humidity, etc.).
A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend on ambient and interior conditions (wind, humidity, etc.).
- Calculate the heat flux (heat loss) through this non-insulated wall.
- Now assume thermal insulation on the outer side of this wall. Use expanded polystyrene insulation 10 cm thick (L2) with the thermal conductivity of k2 = 0.03 W/m.K and calculate the heat flux (heat loss) through this composite wall.
Solution:
As was written, many heat transfer processes involve composite systems and even involve a combination of conduction and convection. It is often convenient to work with an overall heat transfer coefficient, known as a U-factor with these composite systems. The U-factor is defined by an expression analogous to Newton’s law of cooling:
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.
- bare wall
Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 1/30) = 3.53 W/m2K
The heat flux can be then calculated simply as:
q = 3.53 [W/m2K] x 30 [K] = 105.9 W/m2
The total heat loss through this wall will be:
qloss = q . A = 105.9 [W/m2] x 30 [m2] = 3177W
- composite wall with thermal insulation
Assuming one-dimensional heat transfer through the plane composite wall, no thermal contact resistance, and disregarding radiation, the overall heat transfer coefficient can be calculated as:
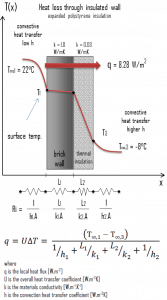 The overall heat transfer coefficient is then:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 0.1/0.03 + 1/30) = 0.276 W/m2K
The heat flux can be then calculated simply as:
q = 0.276 [W/m2K] x 30 [K] = 8.28 W/m2
The total heat loss through this wall will be:
qloss = q . A = 8.28 [W/m2] x 30 [m2] = 248 W
As can be seen, adding a thermal insulator causes a significant decrease in heat losses. It must be added that adding the next layer of the thermal insulator does not cause such high savings. This can be better seen from the thermal resistance method, which can be used to calculate the heat transfer through composite walls. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.