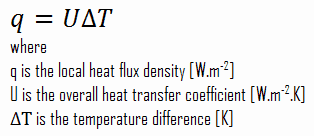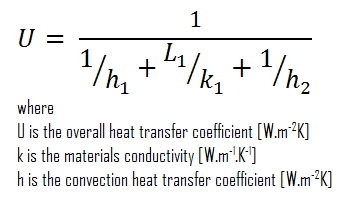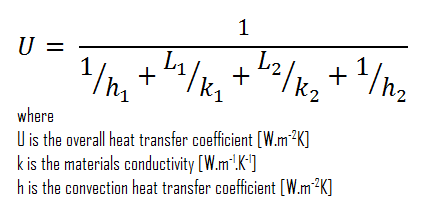Cavity wall insulation is a thermal insulation method used to reduce heat loss through a cavity wall by filling the air space with a thermal insulator. These materials (e.g., polyurethane) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes the heat must be transferred through many interfaces causing a rapid decrease in heat transfer coefficient.
During the construction of new buildings, cavities are often filled with glass wool or rock wool panels placed between the two leaves (sides) of the wall. Polyurethane foam (PUR) is a closed-cell thermoset polymer. Polyurethane foam insulation is available in closed-cell and open-cell formulas. Polyurethane foam can be used as cavity wall insulation or as roof insulation, floor insulation, pipe insulation, and insulation of industrial installations. Insulating panels made from PUR can be applied to all building envelope elements. Another important aspect is that PUR can also be injected into existing cavity walls by using the existing openings and some extra holes.
For existing buildings that were not built with insulated cavities, fibrous material such as cellulose insulation or glass wool is blown into the cavity through suitably drilled holes until it fills the entire wall space. Loose-fill insulation consists of small particles of fiber, foam, or other materials. The most common types of materials used for loose-fill insulation include cellulose, glass wool, and rock wool.
Blown-In and Loose-Fill Insulation
Loose-fill materials can be blown into attics and finished wall cavities. For existing buildings that were not built with insulated cavities, fibrous material such as cellulose insulation or glass wool is blown into the cavity through suitably drilled holes until it fills the entire wall space. Loose-fill insulation consists of small particles of fiber, foam, or other materials. The most common types of materials used for loose-fill insulation include cellulose, glass wool, and rock wool.
- Cellulose insulation is made from recycled paper products, primarily newspapers, and has a very high recycled material content.
- Glass wool (originally known also as fiberglass) is an insulating material made from fibers of glass arranged using a binder into a texture similar to wool.
- Stone wool, also known as rock wool, is based on natural minerals present in large quantities throughout the earth, e.g., volcanic rock, typically basalt or dolomite.
These small particles made from these materials form an insulation material that can conform to any space without disturbing structures or finishes. One of the methods is Wet-spray cellulose insulation. This type of insulation is similar to loose-fill insulation but is applied with a small quantity of water to help the cellulose bind to the inside of open wall cavities.
Example of Insulation – Cellulose Insulation
Cellulose insulation is made from recycled paper products, primarily newspapers, and has a very high recycled material content. The obtained cellulose fibers have a wool-like structure (therefore, paper wool). Boric acid or ammonium sulfate are added to make the cellulose fibers moisture and flame retardant. Cellulose insulation is used in wall and roof cavities to insulate, draught-proof, and reduce free noise. Cellulose insulation is used in new and existing homes, usually as loose fill in open attic installations and dense packed in building cavities. Cellulose and other loose-fill materials can be blown into attics, finished wall cavities, and hard-to-reach areas.
Typical thermal conductivity values for cellulose insulation are between 0.022 and 0.035W/m∙K.
Example – Heat Loss through a Wall
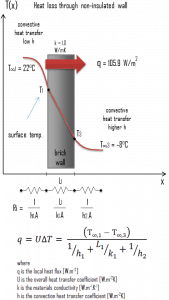 A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend especially on ambient and interior conditions (wind, humidity, etc.).
A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend especially on ambient and interior conditions (wind, humidity, etc.).
- Calculate the heat flux (heat loss) through this non-insulated wall.
- Now assume thermal insulation on the outer side of this wall. Use glass wool insulation 10 cm thick (L2) with the thermal conductivity of k2 = 0.023 W/m.K and calculate the heat flux (heat loss) through this composite wall.
Solution:
As was written, many heat transfer processes involve composite systems and even involve a combination of conduction and convection. It is often convenient to work with an overall heat transfer coefficient, known as a U-factor with these composite systems. The U-factor is defined by an expression analogous to Newton’s law of cooling:
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.
- bare wall
Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 1/30) = 3.53 W/m2K
The heat flux can be then calculated simply as:
q = 3.53 [W/m2K] x 30 [K] = 105.9 W/m2
The total heat loss through this wall will be:
qloss = q . A = 105.9 [W/m2] x 30 [m2] = 3177W
- composite wall with thermal insulation
Assuming one-dimensional heat transfer through the plane composite wall, no thermal contact resistance, and disregarding radiation, the overall heat transfer coefficient can be calculated as:
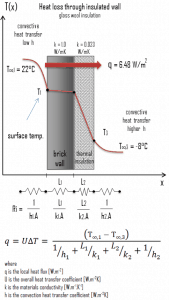 The overall heat transfer coefficient is then:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 0.1/0.023 + 1/30) = 0.216 W/m2K
The heat flux can be then calculated simply as:
q = 0.216 [W/m2K] x 30 [K] = 6.48 W/m2
The total heat loss through this wall will be:
qloss = q . A = 6.48 [W/m2] x 30 [m2] = 194 W
As can be seen, adding a thermal insulator causes a significant decrease in heat losses. It must be added that adding the next layer of the thermal insulator does not cause such high savings. This can be better seen from the thermal resistance method, which can be used to calculate the heat transfer through composite walls. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.