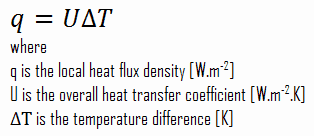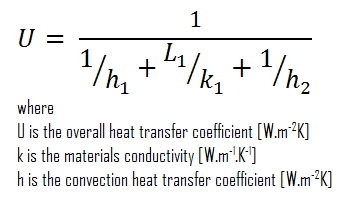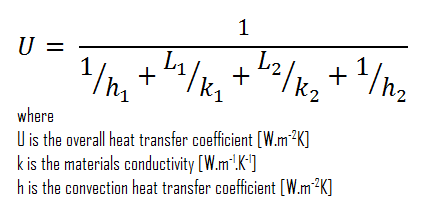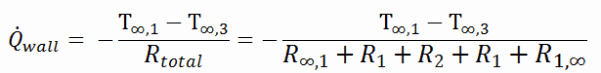Thermal insulations consist of low thermal conductivity materials combined to achieve an even lower system thermal conductivity.
Thermal insulation can be achieved with specially engineered methods or processes and suitable object shapes and materials.
See also: Thermal conductivity
From the microscopic point of view, the transport of thermal energy in solids may generally be due to two effects:
- the migration of free electrons
- lattice vibrational waves (phonons)
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
Metals, in general, have high electrical conductivity and high thermal conductivity. These properties originate because their outer electrons (free electrons) are delocalized. Their contribution to the thermal conductivity is very high and is referred to as the electronic thermal conductivity, ke. As a result, metals are very good thermal conductors instead of thermal insulators.
For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. Lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass.
It must be added that thermal insulation is primarily based on gases’ very low thermal conductivity. Gases possess poor thermal conduction properties compared to liquids and solids and thus make a good insulation material if they can be trapped (e.g., in a foam-like structure). Air and other gases are generally good insulators. But the main benefit is in the absence of convection. Therefore, many insulating materials (e.g., polystyrene) function simply by having many gas-filled pockets, which prevent large-scale convection. Alternation of gas pocket and solid material causes heat to transfer through many interfaces, causing a rapid decrease in heat transfer coefficient.
It must be noted, heat losses from hotter objects occur by three mechanisms (either individually or in combination):
So far, we have not discussed thermal radiation as a mode of heat loss. Radiation heat transfer is mediated by electromagnetic radiation, and therefore it does not require any medium for heat transfer. Energy transfer by radiation is fastest (at the speed of light), and it suffers no attenuation in a vacuum. Any material with a temperature above absolute zero gives off some radiant energy. Most energy of this type is in the infra-red region of the electromagnetic spectrum, although some of it is in the visible region. Materials with low emissivity should be used to decrease this type of heat transfer. The emissivity, ε, of the surface of a material is its effectiveness in emitting energy as thermal radiation and varies between 0.0 and 1.0. In general, polished metals have very low emissivity and therefore are widely used to reflect radiant energy to its source, as in the case of first aid blankets.
Thermal Insulator
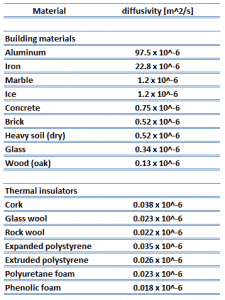As was written, thermal insulation is based on the use of substances with very low thermal conductivity. These materials are known as thermal insulators. Common thermal insulators are wool, fiberglass, rock wool, polystyrene, polyurethane, goose feather, etc. Therefore, these materials are very poor conductors of heat and are good thermal insulators.
It must be added that thermal insulation is primarily based on gases’ very low thermal conductivity. Gases possess poor thermal conduction properties compared to liquids and solids and thus make a good insulation material if they can be trapped (e.g., in a foam-like structure). Air and other gases are generally good insulators. But the main benefit is in the absence of convection. Therefore, many insulating materials (e.g., polystyrene) function simply by having many gas-filled pockets, which prevent large-scale convection. In all types of thermal insulation, evacuation of the air in the void space will further reduce the overall thermal conductivity of the insulator.
Alternation of gas pocket and solid material causes heat to transfer through many interfaces, causing a rapid decrease in heat transfer coefficient.
In the case of thermal radiation insulation, reflective insulations can be used. Reflective insulations are usually composed of multilayered, parallel foils of high reflectivity, spaced to reflect thermal radiation to their source.
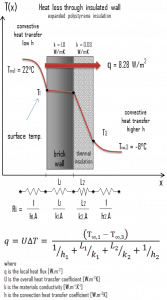
Example – Heat Loss through a Wall
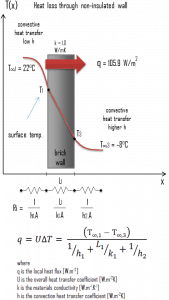A major source of heat loss from a house is through walls. Calculate the rate of heat flux through a wall 3 m x 10 m in the area (A = 30 m2). The wall is 15 cm thick (L1), and it is made of bricks with thermal conductivity of k1 = 1.0 W/m.K (poor thermal insulator). Assume that the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h1 = 10 W/m2K and h2 = 30 W/m2K, respectively. Note that these convection coefficients strongly depend on ambient and interior conditions (wind, humidity, etc.).
- Calculate the heat flux (heat loss) through this non-insulated wall.
- Now assume thermal insulation on the outer side of this wall. Use expanded polystyrene insulation 10 cm thick (L2) with the thermal conductivity of k2 = 0.03 W/m.K and calculate the heat flux (heat loss) through this composite wall.
Solution:
As was written, many heat transfer processes involve composite systems and even involve a combination of conduction and convection. It is often convenient to work with an overall heat transfer coefficient, known as a U-factor with these composite systems. The U-factor is defined by an expression analogous to Newton’s law of cooling:
The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.
- bare wall
Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 1/30) = 3.53 W/m2K
The heat flux can be then calculated simply as:
q = 3.53 [W/m2K] x 30 [K] = 105.9 W/m2
The total heat loss through this wall will be:
qloss = q . A = 105.9 [W/m2] x 30 [m2] = 3177W
- composite wall with thermal insulation
Assuming one-dimensional heat transfer through the plane composite wall, no thermal contact resistance, and disregarding radiation, the overall heat transfer coefficient can be calculated as:
The overall heat transfer coefficient is then:
U = 1 / (1/10 + 0.15/1 + 0.1/0.03 + 1/30) = 0.276 W/m2K
The heat flux can be then calculated simply as:
q = 0.276 [W/m2K] x 30 [K] = 8.28 W/m2
The total heat loss through this wall will be:
qloss = q . A = 8.28 [W/m2] x 30 [m2] = 248 W
As can be seen, adding a thermal insulator causes a significant decrease in heat losses. It must be added that adding the next layer of the thermal insulator does not cause such high savings. This can be better seen from the thermal resistance method, which can be used to calculate the heat transfer through composite walls. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.
