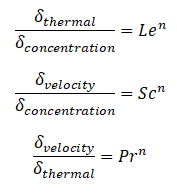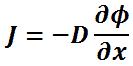The
Lewis number is a dimensionless number named after Warren K. Lewis (1882–1975). The
Lewis number is defined as the ratio of
thermal diffusivity and mass diffusivity. It is used to characterize fluid flows where there is simultaneous heat and mass transfer.
Therefore, the Lewis number is a measure of the relative thermal and concentration boundary layer thicknesses. The Lewis number can also be expressed in terms of the Prandtl number and the Schmidt number as Le = Sc / Pr.
The Lewis number is defined as:
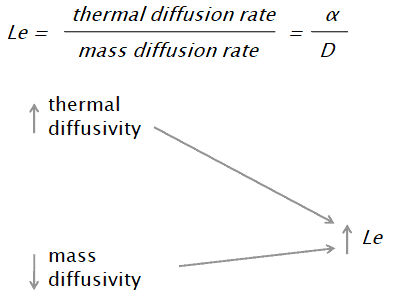
where:
α is thermal diffusivity [m2/s]
D is the mass diffusivity [m2/s]
Similarly, as for Schmidt and Prandtl Number, the Lewis number physically relates the relative thickness of the thermal layer and mass-transfer (concentration) boundary layer.
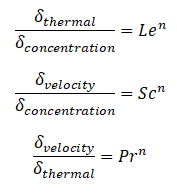
where n = 1/3 for most applications in all three relations. These relations, in general, are applicable only for laminar flow and are not applicable to turbulent boundary layers since turbulent mixing, in this case, may dominate the diffusion processes.
A Lewis number of unity indicates that thermal boundary layer and mass transfer by diffusion are comparable, and temperature and concentration boundary layers almost coincide with each other. Mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion).
Diffusivity is encountered in Fick’s law, which states:
If the concentration of a solute in one region is greater than in another of a solution, the solute diffuses from the region of higher concentration to the region of lower concentration, with a magnitude that is proportional to the concentration gradient.
In one (spatial) dimension, the law is:
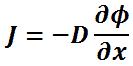
where:
- J is the diffusion flux,
- D is the diffusion coefficient,
- φ (for ideal mixtures) is the concentration.
This law in nuclear reactor theory leads to the diffusion approximation.
References:
Heat Transfer:
- Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
- U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
- Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.
See above:
Introduction to Heat Transfer