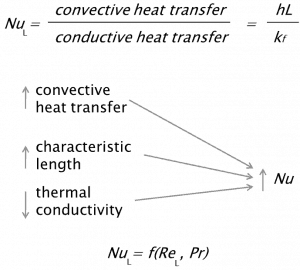
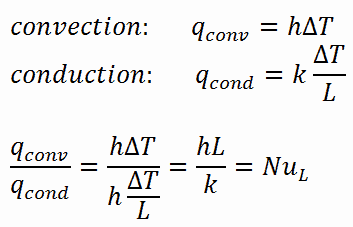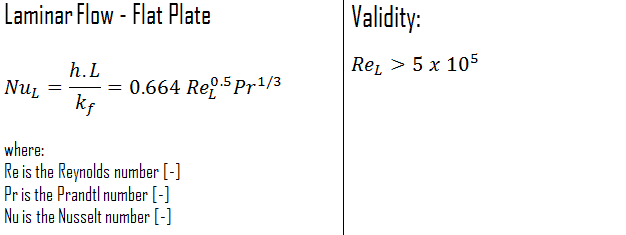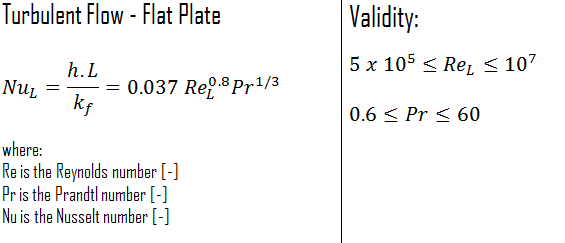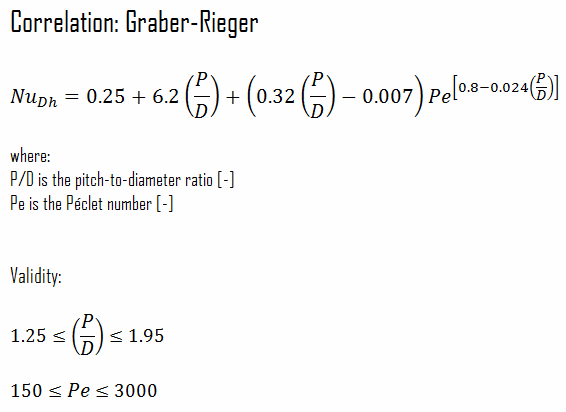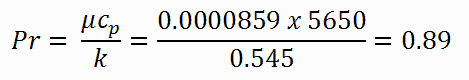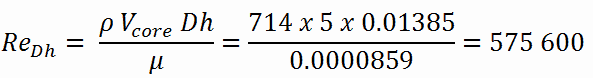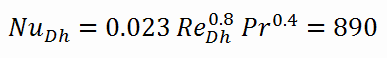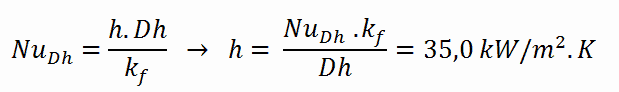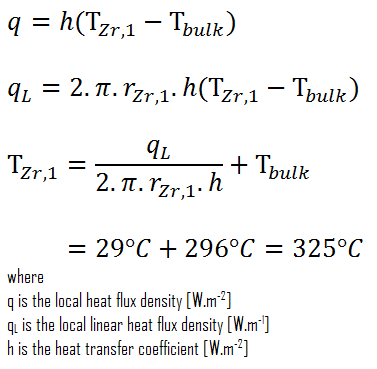The Nusselt number is named after a German engineer Wilhelm Nusselt. The conductive component is measured under the same conditions as the heat convection but with stagnant fluid. The Nusselt number is to the thermal boundary layer what the friction coefficient is to the velocity boundary layer. Thus, the Nusselt number is defined as:
where:
kf is a thermal conductivity of the fluid [W/m.K]
L is the characteristic length
h is the convective heat transfer coefficient [W/m2.K]
For illustration, consider a fluid layer of thickness L and temperature difference ΔT. Heat transfer through the fluid layer will be by convection when the fluid involves some motion and conduction when the fluid layer is motionless.
In the case of conduction, the heat flux can be calculated using Fourier’s law of conduction. In the case of convection, the heat flux can be calculated using Newton’s law of cooling. Taking their ratio gives:
The preceding equation defines the Nusselt number. Therefore, the Nusselt number represents the enhancement of heat transfer through a fluid layer due to convection relative to conduction across the same fluid layer. A Nusselt number of Nu=1 for a fluid layer represents heat transfer across the layer by pure conduction. The larger the Nusselt number, the more effective the convection. A larger Nusselt number corresponds to more effective convection, with turbulent flow typically in the 100–1000 range. The Nusselt number is usually a function of the Reynolds number and the Prandtl number for turbulent flow.
Correlations – Single-phase Fluid Flow
External Laminar Flow
The average Nusselt number over the entire plate is determined by:
This relation gives the average heat transfer coefficient for the entire plate when the flow is laminar over the entire plate.
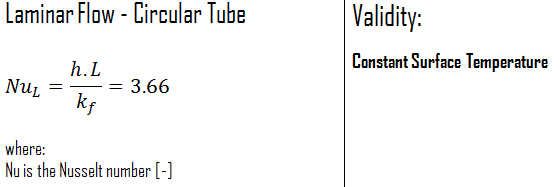
Internal Laminar Flow
Constant Surface Temperature
In laminar flow in a tube with constant surface temperature, both the friction factor and the heat transfer coefficient remain constant in the fully developed region.
Constant Surface Heat Flux
Therefore, for fully developed laminar flow in a circular tube subjected to constant surface heat flux, the Nusselt number is a constant. There is no dependence on the Reynolds or the Prandtl numbers.
External Turbulent Flow
The average Nusselt number over the entire plate is determined by:
This relation gives the average heat transfer coefficient for the entire plate only when the flow is turbulent over the entire plate or when the laminar flow region of the plate is too small relative to the turbulent flow region.
Internal Turbulent Flow – Dittus-Boelter
See also: Dittus-Boelter Equation
For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus-Boelter equation. The Dittus-Boelter equation is easy to solve but is less accurate when there is a large temperature difference across the fluid and is less accurate for rough tubes (many commercial applications) since it is tailored to smooth tubes.
The Dittus-Boelter correlation may be used for small to moderate temperature differences, Twall – Tavg, with all properties evaluated at an, averaged temperature Tavg.
For flows characterized by large property variations, the corrections (e.g., a viscosity correction factor μ/μwall) must be taken into account, for example, as Sieder and Tate recommend.
Nusselt Number for Liquid Metal Reactors
See also: Nusselt Number for Liquid Metal Reactors
For liquid metals, the Prandtl number is very small, generally in the range from 0.01 to 0.001. This means that the thermal diffusivity, which is related to the rate of heat transfer by conduction, unambiguously dominates. This very high thermal diffusivity results from metals’ very high thermal conductivity, which is about 100 times higher than that of water. The Prandtl number for sodium at a typical operating temperature in the Sodium-cooled fast reactors is about 0.004. For this case, the thermal boundary layer development is much more rapid than that of the velocity boundary layer (δt >> δ), and it is reasonable to assume uniform velocity throughout the thermal boundary layer.
Heat transfer coefficients for sodium flow through the fuel channel are based on the Prandtl number and Péclet number. Pitch-to-diameter (P/D) also enters many calculations of heat transfer in liquid metal reactors. Convective heat transfer correlations are usually presented in terms of Nusselt number versus Péclet number. The typical Péclet number for normal operation is from 150 to 300 in the fuel bundles. As for other flow regimes, the Nusselt number and a given correlation can be used to determine the convective heat transfer coefficient.
Example – Nusselt Number – Cladding Surface Temperature
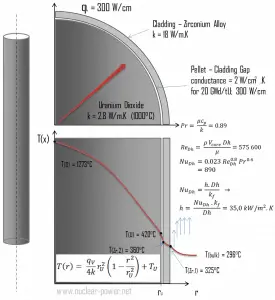 Cladding is the outer layer of the fuel rods, standing between the reactor coolant and the nuclear fuel (i.e., fuel pellets). It is corrosion-resistant material with a low absorption cross-section for thermal neutrons, usually zirconium alloy. Cladding prevents radioactive fission products from escaping the fuel matrix into the reactor coolant and contaminating it. Cladding constitutes one of the barriers in the ‘defense-in-depth ‘approach; therefore, its coolability is one of the key safety aspects.
Cladding is the outer layer of the fuel rods, standing between the reactor coolant and the nuclear fuel (i.e., fuel pellets). It is corrosion-resistant material with a low absorption cross-section for thermal neutrons, usually zirconium alloy. Cladding prevents radioactive fission products from escaping the fuel matrix into the reactor coolant and contaminating it. Cladding constitutes one of the barriers in the ‘defense-in-depth ‘approach; therefore, its coolability is one of the key safety aspects.
Consider the fuel cladding of inner radius rZr,2 = 0.408 cm and outer radius rZr,1 = 0.465 cm. Compared to fuel pellet, there is almost no heat generation in the fuel cladding (cladding is slightly heated by radiation). All heat generated in the fuel must be transferred via conduction through the cladding, and therefore the inner surface is hotter than the outer surface.
Assume that:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the pitch of fuel pins is: p = 13 mm
- the thermal conductivity of saturated water at 300°C is: kH2O = 0.545 W/m.K
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the fluid density is: ρ = 714 kg/m3
- the specific heat is: cp = 5.65 kJ/kg.K
- the core flow velocity is constant and equal to Vcore = 5 m/s
- the temperature of reactor coolant at this axial coordinate is: Tbulk = 296°C
- the linear heat rate of the fuel is qL = 300 W/cm (FQ ≈ 2.0) and thus the volumetric heat rate is qV = 597 x 106 W/m3
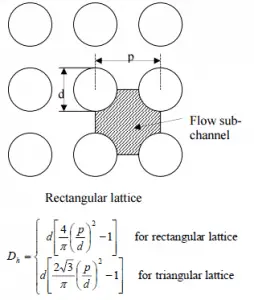 Calculate the Prandtl, Reynolds and Nusselt number for this flow regime (internal forced turbulent flow) inside the rectangular fuel lattice (fuel channel), then calculate the heat transfer coefficient and finally the cladding surface temperature, TZr,1.
Calculate the Prandtl, Reynolds and Nusselt number for this flow regime (internal forced turbulent flow) inside the rectangular fuel lattice (fuel channel), then calculate the heat transfer coefficient and finally the cladding surface temperature, TZr,1.
To calculate the cladding surface temperature, we have to calculate the Prandtl, Reynolds, and Nusselt number because the heat transfer for this flow regime can be described by the Dittus-Boelter equation, which is:
Calculation of the Prandtl number
To calculate the Prandtl number, we have to know:
- the thermal conductivity of saturated water at 300°C is: kH2O = 0.545 W/m.K
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the specific heat is: cp = 5.65 kJ/kg.K
Note that all these parameters significantly differ for water at 300°C from those at 20°C. Prandtl number for water at 20°C is around 6.91. Prandtl number for reactor coolant at 300°C is then:
Calculation of the Reynolds number
To calculate the Reynolds number, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm (to calculate the hydraulic diameter)
- the pitch of fuel pins is: p = 13 mm (to calculate the hydraulic diameter)
- the dynamic viscosity of saturated water at 300°C is: μ = 0.0000859 N.s/m2
- the fluid density is: ρ = 714 kg/m3
The hydraulic diameter, Dh, is a commonly used term when handling flow in non-circular tubes and channels. The hydraulic diameter of the fuel channel, Dh, is equal to 13,85 mm.
See also: Hydraulic Diameter
The Reynolds number inside the fuel channel is then equal to:
This fully satisfies the turbulent conditions.
Calculation of the Nusselt number using Dittus-Boelter equation
For fully developed (hydrodynamically and thermally) turbulent flow in a smooth circular tube, the local Nusselt number may be obtained from the well-known Dittus-Boelter equation.
To calculate the Nusselt number, we have to know:
- the Reynolds number, which is ReDh = 575600
- the Prandtl number, which is Pr = 0.89
The Nusselt number for the forced convection inside the fuel channel is then equal to:
Calculation of the heat transfer coefficient and the cladding surface temperature, TZr,1
Detailed knowledge of geometry, fluid parameters, the outer radius of cladding, linear heat rate, convective heat transfer coefficient allows us to calculate the temperature difference ∆T between the coolant (Tbulk) and the cladding surface (TZr,1).
To calculate the cladding surface temperature, we have to know:
- the outer diameter of the cladding is: d = 2 x rZr,1 = 9,3 mm
- the Nusselt number, which is NuDh = 890
- the hydraulic diameter of the fuel channel is Dh = 13,85 mm
- the thermal conductivity of reactor coolant (300°C) is: kH2O = 0.545 W/m.K
- the bulk temperature of reactor coolant at this axial coordinate is Tbulk = 296°C
- the linear heat rate of the fuel is: qL = 300 W/cm (FQ ≈ 2.0)
The convective heat transfer coefficient, h, is given directly by the definition of Nusselt number:
Finally, we can calculate the cladding surface temperature (TZr,1) simply using Newton’s Law of Cooling:
For PWRs at normal operation, there is compressed liquid water inside the reactor core, loops, and steam generators. The pressure is maintained at approximately 16MPa. At this pressure, water boils at approximately 350°C(662°F). As can be seen, the surface temperature TZr,1 = 325°C ensures that even subcooled boiling does not occur. Note that subcooled boiling requires TZr,1 = Tsat. Since the inlet temperatures of the water are usually about 290°C (554°F), it is obvious this example corresponds to the lower part of the core. At higher core elevations, the bulk temperature may reach up to 330°C. The temperature difference of 29°C causes the subcooled boiling may occur (330°C + 29°C > 350°C). On the other hand, nucleate boiling at the surface effectively disrupts the stagnant layer. Therefore, nucleate boiling significantly increases the ability of a surface to transfer thermal energy to the bulk fluid. As a result, the convective heat transfer coefficient significantly increases, and therefore at higher elevations, the temperature difference (TZr,1 – Tbulk) significantly decreases.