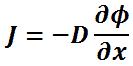Peclet Number in Mass Transfer
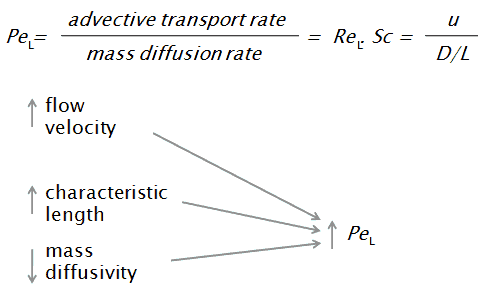
In mass transfer problems, the Péclet number is the product of the Reynolds number, which describes the flow regime, and the Schmidt number, which is used to characterize fluid flows with simultaneous momentum and mass diffusion convection processes.
where:
- u is the flow velocity,
- L is a characteristic linear dimension (traveled length of the fluid; hydraulic diameter etc.)
- D is the mass diffusivity [m2/s]
Peclet Number in Heat Transfer
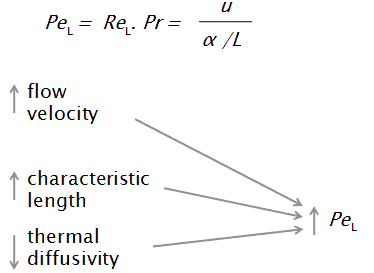
In heat transfer problems, the Péclet number is the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid. The Péclet number is simply defined as the product of the Reynolds number, which describes the flow regime, and the Prandtl number, which describes the relationship between momentum diffusivity and thermal diffusivity. If Pe is small, conduction is important.
where:
- u is the flow velocity,
- L is a characteristic linear dimension (traveled length of the fluid; hydraulic diameter etc.)
- α is thermal diffusivity [m2/s]
Thermal diffusivity represents how fast heat diffuses through the material and has units m2/s. In other words, it is the measure of the thermal inertia of given material. Thermal diffusivity is usually denoted α and is given by:
As can be seen, it measures the ability of a material to conduct thermal energy(represented by factor k) relative to its ability to store thermal energy (represented by factor ρ.cp). Materials of large α will respond quickly to changes in their thermal environment. In contrast, materials of small α will respond more slowly (heat is mostly absorbed), taking longer to reach a new equilibrium condition.
Mass Diffusivity and Fick’s law
Diffusivity is encountered in Fick’s law, which states:
If the concentration of a solute in one region is greater than in another of a solution, the solute diffuses from the region of higher concentration to the region of lower concentration, with a magnitude that is proportional to the concentration gradient.
In one (spatial) dimension, the law is:
where:
- J is the diffusion flux,
- D is the diffusion coefficient,
- φ (for ideal mixtures) is the concentration.
The use of this law in nuclear reactor theory leads to the diffusion approximation.