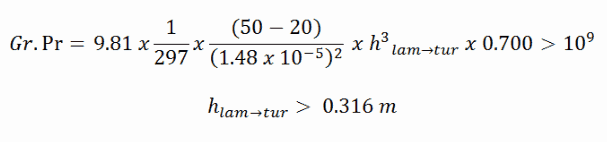Facebook Instagram Youtube Twitter

What is Rayleigh Number

The Rayleigh number is a dimensionless number named after  Lord Rayleigh. The Rayleigh number is closely related to the Grashof number, and both numbers are used to describe natural convection (Gr) and heat transfer by natural convection (Ra).

The Rayleigh number is simply defined as the product of the Grashof number, which describes the relationship between buoyancy and viscosity within a fluid, and the Prandtl number, which describes the relationship between momentum diffusivity and thermal diffusivity.

Rax = Grx . Pr

The Grashof number is defined as the ratio of the buoyant to a viscous force acting on a fluid in the velocity boundary layer. Its role in natural convection is much like that of the Reynolds number in forced convection. Natural convection occurs if this motion and mixing are caused by density variations resulting from temperature differences within the fluid. Usually, the density decreases due to increased temperature and causes the fluid to rise. This motion is caused by the buoyant force. The major force that resists the motion is the viscous force. The Grashof number is a way to quantify the opposing forces.

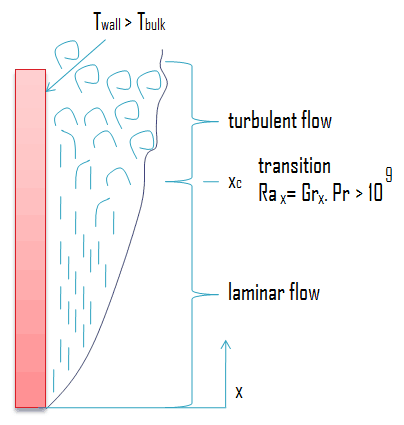
The Rayleigh number is used to express heat transfer in natural convection. The magnitude of the Rayleigh number is a good indication of whether the natural convection boundary layer is laminar or turbulent. The simple empirical correlations for the average Nusselt number, Nu, in natural convection are of the form:

Nux = C. Raxn

The values of the constants C and n depend on the geometry of the surface and the flow regime, which is characterized by the range of the Rayleigh number. The value of n is usually n = 1/4 for laminar flow and n = 1/3 for turbulent flow.

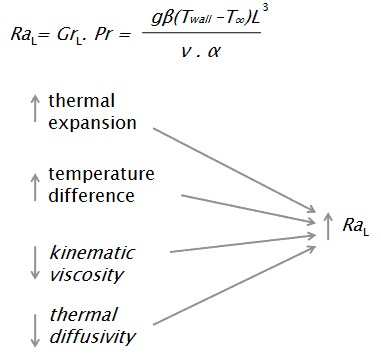
The Rayleigh number is defined as:

rayleigh number - definition - formula

where:

g is the acceleration due to Earth’s gravity

β is the coefficient of thermal expansion

Twall is the wall temperature

T∞ is the bulk temperature

L is the vertical length

α is the thermal diffusivity

ν is the kinematic viscosity.

For gases β = 1/T where the temperature is in K. For liquids, β can be calculated if the variation of density with the temperature at constant pressure is known. For a vertical flat plate, the flow turns turbulent for the value of:

Rax = Grx . Pr > 109 

As in forced convection, the microscopic nature of flow and convection correlations are distinctly different in the laminar and turbulent regions.

Example: Rayleigh Number

Rayleigh Number and Grashof NumberA vertical plate is maintained at 50°C in 20°C air. Determine the height at which the boundary layer will turn turbulent if turbulence sets in at Ra = Gr.Pr = 109.

Solution:

The property values required for this example are:

ν = 1.48 x 10-5 m2/s

ρ = 1.17 kg/m3

Pr = 0.700

β = 1/ (273 + 20) = 1/293

We know the natural circulation becomes turbulent at approximately Ra = Gr.Pr > 109, which is fulfilled at the following height:

grashof number - example

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Characteristic Numbers