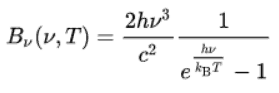The term blackbody was introduced by German physicist Gustav Kirchhoff in 1860. Blackbody radiation is also called thermal radiation, cavity radiation, complete radiation, or temperature radiation. The following laws are associated with blackbody radiation:
- Kirchhoff’s law. This law gives the relationship between the emissivity and absorptivity of an object.
- Planck’s law. This law describes the spectrum of blackbody radiation, which depends only on the object’s temperature.
- Wien’s displacement law. This law determines the most likely frequency of the emitted radiation.
- Stefan–Boltzmann law. This law gives the radiant intensity.
It is known that the amount of radiation energy emitted from a surface at a given wavelength depends on the material of the body and the condition of its surface, as well as the surface temperature. Therefore, various materials emit different amounts of radiant energy even when they are at the same temperature. A body that emits the maximum amount of heat for its absolute temperature is called a blackbody.
A blackbody is an idealized physical body that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies.
The surface of a blackbody emits thermal radiation at the rate of approximately 448 watts per square meter at room temperature (25 °C, 298.15 K). Real objects with emissivities less than 1.0 (e.g., copper wire) emit radiation at correspondingly lower rates (e.g., 448 x 0.03 = 13.4 W/m2). Emissivity plays an important role in heat transfer problems. For example, solar heat collectors incorporate selective surfaces with very low emissivities. These collectors waste very little solar energy through the emission of thermal radiation.
Since the absorptivity and the emissivity are interconnected by Kirchhoff’s Law of thermal radiation, a blackbody is also a perfect absorber of electromagnetic radiation.
Kirchhoff’s Law of thermal radiation:
For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
A blackbody absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence, and its absorptivity is equal to unity, which is also the highest possible value. A blackbody is a perfect absorber (and a perfect emitter).
Note that visible radiation occupies a very narrow spectrum band from 400 to 760 nm. We cannot make any judgments about the blackness of a surface based on visual observations. For example, consider a white paper that reflects visible light and thus appears white. On the other hand, it is essentially black for infrared radiation (absorptivity α = 0.94) since they strongly absorb long-wavelength radiation.
Blackbody Emissive Power
The blackbody emissive power, Eb [W/m2], from a blackbody to its surroundings is proportional to the fourth power of the absolute temperature and can be expressed by the following equation:
Eb = σT4
where σ is a fundamental physical constant called the Stefan–Boltzmann constant, equal to 5.6697×10-8 W/m2K4, and T is the absolute temperature of the surface in K.
The term blackbody was introduced by German physicist Gustav Kirchhoff in 1860. Blackbody radiation is also called thermal radiation, cavity radiation, complete radiation, or temperature radiation. The following laws are associated with blackbody radiation:
- Kirchhoff’s law. This law gives the relationship between the emissivity and absorptivity of an object.
- Planck’s law. This law describes the spectrum of blackbody radiation, which depends only on the object’s temperature.
- Wien’s displacement law. This law determines the most likely frequency of the emitted radiation.
- Stefan–Boltzmann law. This law gives the radiant intensity.
All bodies above absolute zero temperature radiate some heat, and the sun and earth both radiate heat toward each other. This seems to violate the Second Law of Thermodynamics, which states that heat cannot spontaneously flow from cold system to hot system without external work being performed on the system. The paradox is resolved because each body must be in direct sight of the other to receive radiation from it. Therefore, whenever the cool body is radiating heat to the hot body, the hot body must also be radiating heat to the cool body. Moreover, a hot body will radiate more energy than a cold body. The case of different emissivities is solved by Kirchhoff’s Law of thermal radiation, which states that objects with low emissivity also have low absorptivity. As a result, heat cannot spontaneously flow from cold system to hot system, and the second law is still satisfied.
Spectrum – Blackbody Radiation
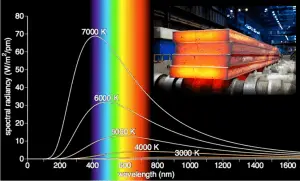
The Stefan–Boltzmann law determines the total blackbody emissive power, Eb, the sum of the radiation emitted over all wavelengths. Planck’s law describes the spectrum of blackbody radiation, which depends only on the object’s temperature and relates the spectral blackbody emissive power, Ebλ. This law is named after a German theoretical physicist Max Planck, who proposed it in 1900. Planck’s law is a pioneering result of modern physics and quantum theory. Planck’s hypothesis that energy is radiated and absorbed in discrete “quanta” (or energy packets) precisely matched the observed patterns of blackbody radiation and resolved the ultraviolet catastrophe.
Using this hypothesis, Planck showed that the spectral radiance of a body for frequency ν at absolute temperature T is given by:
where
- Bν(v, T) is the spectral radiance (the power per unit solid angle and unit of area normal to the propagation) density of frequency ν radiation per unit frequency at thermal equilibrium at temperature T
- h is the Planck constant
- c is the speed of light in a vacuum
- kB is the Boltzmann constant
- ν is the frequency of the electromagnetic radiation
- T is the absolute temperature of the body
Planck’s law has the following important features:
- The emitted radiation varies continuously with wavelength.
- At any wavelength, the magnitude of the emitted radiation increases with increasing temperature.
- The spectral region where the radiation is concentrated depends on temperature, with comparatively more radiation appearing at shorter wavelengths as the temperature increases (Wien’s Displacement Law).
