According to the Stefan–Boltzmann law:
Radiation heat transfer rate, q [W/m2], from a body (e.g., a black body) to its surroundings is proportional to the fourth power of the absolute temperature. It can be expressed by the following equation:
q = εσT4
where σ is a fundamental physical constant called the Stefan–Boltzmann constant, equal to 5.6697×10-8 W/m2K4.
The Stefan–Boltzmann constant is named after Josef Stefan (who discovered the Stefa-Boltzman law experimentally in 1879) and Ludwig Boltzmann (who derived it theoretically soon after). As can be seen, radiation heat transfer is important at very high temperatures and in a vacuum.
Emissivity
The
emissivity, ε, of the surface of a material is its effectiveness in emitting energy as
thermal radiation and varies between 0.0 and 1.0.
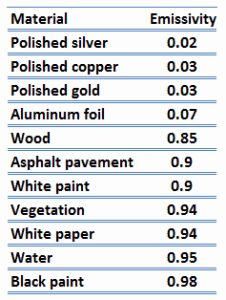 By definition, a blackbody in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies. The Stefan-Boltzmann law must include emissivity to consider the fact that real objects are gray bodies. Quantitatively, emissivity is the ratio of the thermal radiation from a surface to the radiation from an ideal black surface at the same temperature as given by the Stefan–Boltzmann law. Emissivity is simply a factor by which we multiply the black body heat transfer to consider that the black body is the ideal case.
By definition, a blackbody in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies. The Stefan-Boltzmann law must include emissivity to consider the fact that real objects are gray bodies. Quantitatively, emissivity is the ratio of the thermal radiation from a surface to the radiation from an ideal black surface at the same temperature as given by the Stefan–Boltzmann law. Emissivity is simply a factor by which we multiply the black body heat transfer to consider that the black body is the ideal case.
The surface of a blackbody emits thermal radiation at the rate of approximately 448 watts per square meter at room temperature (25 °C, 298.15 K). Real objects with emissivities less than 1.0 (e.g., copper wire) emit radiation at correspondingly lower rates (e.g., 448 x 0.03 = 13.4 W/m2). Emissivity plays an important role in heat transfer problems. For example, solar heat collectors incorporate selective surfaces with very low emissivities. These collectors waste very little solar energy through the emission of thermal radiation.
Absorptivity
Another important radiation property of a surface is its
absorptivity,
α, which is the fraction of the radiation energy incident on a surface that is absorbed by the surface. Like emissivity, value of absorptivity is in the range 0 < α < 1.
From its definition, a blackbody, which is an idealized physical body, absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. That is, a blackbody is a perfect absorber. Since the absorptivity is less than unity for real objects, a real object can not absorb all incident light. The incomplete absorption can be due to some of the incident light being transmitted through the body or to some of it being reflected at the body’s surface.
In general, the absorptivity and the emissivity are interconnected by Kirchhoff’s Law of thermal radiation, which states:
For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
emissivity ε = absorptivity α
Note that visible radiation occupies a very narrow spectrum band from 400 to 760 nm. We cannot make any judgments about the blackness of a surface based on visual observations. For example, consider a white paper that reflects visible light and thus appears white. On the other hand, it is essentially black for infrared radiation (absorptivity α = 0.94) since they strongly absorb long-wavelength radiation.
As was written, the
Stefan–Boltzmann law gives the radiant intensity of a single object. But using the
Stefan–Boltzmann law, we can also determine the radiation heat transfer between two objects. Two bodies that radiate toward each other have a net heat flux between them. The net flow rate of heat between them is given by:
Q = εσA1-2(T41 −T42) [J/s]
q = εσ(T41 −T42) [J/m2s]
The area factor A1-2 is the area viewed by body 2 of body 1 and can become fairly difficult to calculate.
Blackbody Radiation
It is known that the amount of radiation energy emitted from a surface at a given wavelength depends on the material of the body and the condition of its surface, as well as the surface temperature. Therefore, various materials emit different amounts of radiant energy even when they are at the same temperature. A body that emits the maximum amount of heat for its absolute temperature is called a blackbody.
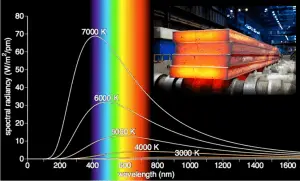 A blackbody is an idealized physical body that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies.
A blackbody is an idealized physical body that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies.
The surface of a blackbody emits thermal radiation at the rate of approximately 448 watts per square meter at room temperature (25 °C, 298.15 K). Real objects with emissivities less than 1.0 (e.g., copper wire) emit radiation at correspondingly lower rates (e.g., 448 x 0.03 = 13.4 W/m2). Emissivity plays an important role in heat transfer problems. For example, solar heat collectors incorporate selective surfaces with very low emissivities. These collectors waste very little solar energy through the emission of thermal radiation.
Since the absorptivity and the emissivity are interconnected by Kirchhoff’s Law of thermal radiation, a blackbody is also a perfect absorber of electromagnetic radiation.
Kirchhoff’s Law of thermal radiation:
For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
emissivity ε = absorptivity α
A blackbody absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Therefore, its absorptivity is equal to unity, which is also the highest possible value. A blackbody is a perfect absorber (and a perfect emitter).
Note that visible radiation occupies a very narrow band of the spectrum from 400 to 760 nm. We cannot make any judgments about the blackness of a surface based on visual observations. For example, consider a white paper that reflects visible light and thus appears white. On the other hand, it is essentially black for infrared radiation (absorptivity α = 0.94) since they strongly absorb long-wavelength radiation.
References:
Heat Transfer:
- Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
- Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.
 A blackbody is an idealized physical body that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies.
A blackbody is an idealized physical body that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body, and they radiate less heat than a black body and therefore are called gray bodies.