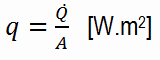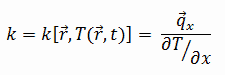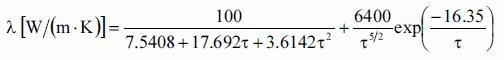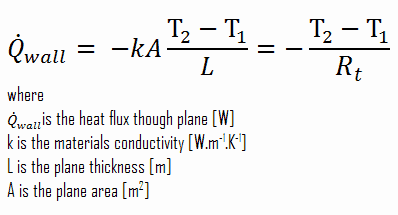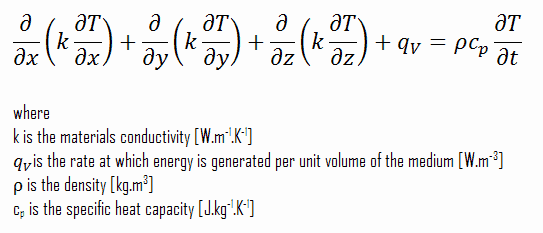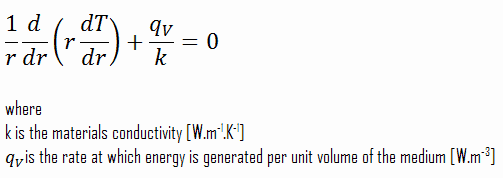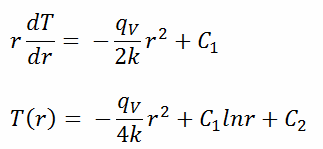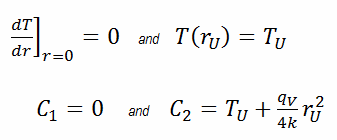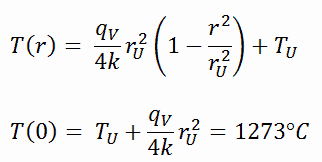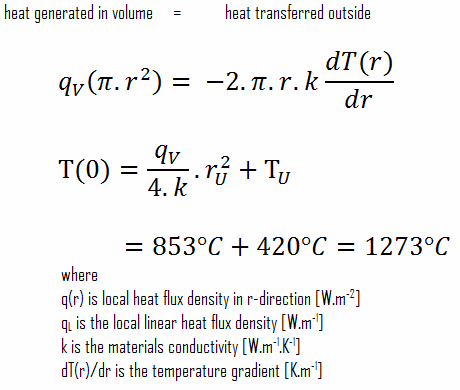Article Summary & FAQs
What is thermal conduction?
Thermal conduction also called heat conduction, is one of the heat transfer mechanisms that occur within a body or between two bodies in contact without the involvement of mass flow and mixing. It is the direct microscopic exchange of kinetic energy of particles through the boundary between two systems.
Key Facts
Heat is the amount of energy flowing spontaneously from one body to another due to its temperature difference. Heat is a form of energy, but it is energy in transit.
Heat transfer by conduction depends on the driving “force” of the temperature difference and the thermal conductivity (or the resistance to heat transfer).
Fourier’s law of thermal conduction law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area at right angles to that gradient through which the heat flows.
Metals, in general, have high electrical conductivity high thermal conductivity. The thermal conductivities of metals originate from the fact that their outer electrons are delocalized.
Thermal insulators have very low thermal conductivity. Their low thermal conductivity is based on the alternation of gas pocket and solid material that causes the heat must be transferred through many interfaces causing a rapid decrease in heat transfer coefficient.
The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials.
Thermal conduction, also called heat conduction, occurs within a body or between two bodies in contact without the involvement of mass flow and mixing. It is the direct microscopic exchange of kinetic energy of particles through the boundary between two systems. Heat transfer by conduction depends on the driving “force” of the temperature difference and the thermal conductivity (or the resistance to heat transfer). The thermal conductivity depends on the nature and dimensions of the heat transfer medium. All heat transfer problems involve the temperature difference, geometry, and the physical properties of the object being studied. In conduction heat transfer problems, the studied object is usually solid.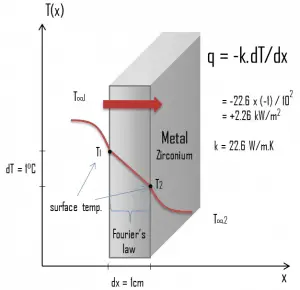
Microscopically this mode of energy transfer is attributed to free-electron flow from higher to lower energy levels, lattice vibration, and molecular collision. Consider a block of stone at high temperature that consists of atoms oscillating intensely around their average positions. At low temperatures, the atoms continue to oscillate but with less intensity.
If a hotter block of stone is put in contact with a cooler block, the intensely oscillating atoms at the edge of the hotter block give off their kinetic energy to the less oscillating atoms at the edge of the cool block. In this case, there is energy transfer between these two blocks, and heat flows from the hotter to the cooler block by these random vibrations. The modern view ascribes the energy transfer to lattice waves induced by atomic motion. In electrical insulators, the energy transfer is exclusive via these lattice waves. In a conductor, it is also due to the translational motion of the free electrons.
See also: Zeroth Law of Thermodynamics
In general, metals are usually good conductors of thermal energy, and it is closely associated with their good electrical conductivity. For metals, the thermal conductivity is quite high, and those metals which are the best electrical conductors are also the best thermal conductors. This is due to the way that metals bond chemically. Metallic bonds have free-moving electrons (free electrons) that transfer thermal energy rapidly through the metal. The electron fluid of a conductive metallic solid conducts most of the heat flux through the solid. Phonon flux is still present but carries less energy. These mechanisms of thermal conduction will be discussed later.
Fourier’s law of Thermal Conduction
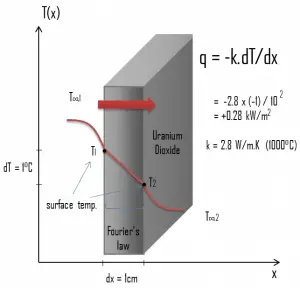
Heat transfer processes can be quantified in terms of appropriate rate equations. The rate equation in this heat transfer mode is based on Fourier’s law of thermal conduction. This law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area, at right angles to that gradient, through which the heat flows. Its differential form is:
where A is the heat transfer area. The unit of heat flux in English units is Btu/h·ft2. Note that heat flux may vary with time and position on a surface.
In nuclear reactors, limitations of the local heat flux are of the highest importance for reactor safety. Since nuclear fuel consists of fuel rods, the heat flux is defined in units of W/cm (local linear heat flux) or kW/rod (power per fuel rod).
The proportionality constant obtained in the relation is known as thermal conductivity, k (or λ), of the material. A material that readily transfers energy by conduction is a good thermal conductor and has a high value of k. Fourier’s law is an expression that defines thermal conductivity.
As can be seen, solve Fourier’s law, we have to involve the temperature difference, the geometry, and the thermal conductivity of the object. This law was first formulated by Joseph Fourier in 1822, who concluded that “the heat flux resulting from thermal conduction is proportional to the magnitude of the temperature gradient and opposite to it in sign”.
Similarly, as Fourier’s law determines the heat flux through a slab, it can also be used to determine the temperature difference when q is known. This can be used to calculate the temperature in the center of the fuel pellet, as will be shown in the following sections.
Thermal Conductivity
The heat transfer characteristics of solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It measures a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies to all matter, regardless of its state (solid, liquid, or gas). Therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature, and for vapors, it also depends upon pressure. In general:
Most materials are nearly homogeneous; therefore, we usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material, the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
The previous equation follows that the conduction heat flux increases with increasing thermal conductivity and increases with increasing temperature differences. In general, the thermal conductivity of a solid is larger than that of a liquid, which is larger than that of a gas. This trend is due largely to differences in intermolecular spacing for the two states of matter. In particular, diamond has the highest hardness and thermal conductivity of any bulk material.
See also: Thermal Conductivity
Most of PWRs use uranium fuel, which is in the form of uranium dioxide. Uranium dioxide is a black semiconducting solid with very low thermal conductivity. On the other hand, uranium dioxide has a very high melting point and has well-known behavior. The UO2 is pressed into pellets, and these pellets are then sintered into the solid.
These pellets are then loaded and encapsulated within a fuel rod (or fuel pin) made of zirconium alloys due to their very low absorption cross-section (unlike stainless steel). The surface of the tube, which covers the pellets, is called fuel cladding. Fuel rods are the base element of a fuel assembly.
The thermal conductivity of uranium dioxide is very low compared with metal uranium, uranium nitride, uranium carbide, and zirconium cladding material. Thermal conductivity is one of the parameters which determine the fuel centerline temperature. This low thermal conductivity can result in localized overheating in the fuel centerline, and therefore this overheating must be avoided. Overheating of the fuel is prevented by maintaining the steady-state peak linear heat rate (LHR) or the Heat Flux Hot Channel Factor – FQ(z) below the level at which fuel centerline melting occurs. Expansion of the fuel pellet upon centerline melting may cause the pellet to stress the cladding to the point of failure.
Thermal conductivity of solid UO2 with a density of 95% is estimated by the following correlation [Klimenko; Zorin]:
where τ = T/1000. The uncertainty of this correlation is +10% in the range from 298.15 to 2000 K and +20% in the range from 2000 to 3120 K.
Special reference: Thermal and Nuclear Power Plants/Handbook ed. by A.V. Klimenko and V.M. Zorin. MEI Press, 2003.
Special reference: Thermophysical Properties of Materials For Nuclear Engineering: A Tutorial and Collection of Data. IAEA-THPH, IAEA, Vienna, 2008. ISBN 978–92–0–106508–7.
In engineering, another very important concept is often used. Since there is an analogy between the diffusion of heat and electrical charge, engineers often use thermal resistance (i.e., thermal resistance against heat conduction) to calculate the heat transfer through materials. Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.
Consider a plane wall of thickness L and average thermal conductivity k. The two surfaces of the wall are maintained at constant temperatures of T1 and T2. For one-dimensional steady heat conduction through the wall, we have T(x). Then Fourier’s law of heat conduction for the wall can be expressed as:
Heat Conduction Equation
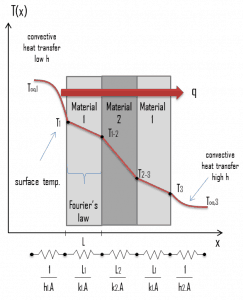
In previous sections, we have dealt with one-dimensional steady-state heat transfer, characterized by Fourier’s law of heat conduction. But its applicability is very limited. This law assumes steady-state heat transfer through a planar body (note that Fourier’s law can also be derived for cylindrical and spherical coordinates) without heat sources. The rate equation is simply in this heat transfer mode, where the temperature gradient is known.
But a major problem in most conduction analyses is determining the temperature field in a medium resulting from conditions imposed on its boundaries. In engineering, we have to solve heat transfer problems involving different geometries and conditions, such as a cylindrical nuclear fuel element, which involves an internal heat source or the wall of a spherical containment. These problems are more complex than the planar analyses in previous sections. Therefore these problems will be the subject of this section, in which the heat conduction equation will be introduced and solved.
See also: Heat Equation
Heat Conduction Equation – General Form
The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials. Once this temperature distribution is known, the conduction heat flux at any point in the material or on its surface may be computed from Fourier’s law.
The heat equation is derived from Fourier’s law and conservation of energy. Fourier’s law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area at right angles to that gradient, through which the heat flows.
A change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. That is:
∆Q = ρ.cp.∆T
General Form
Using these two equations, we can derive the general heat conduction equation:
This equation is also known as the Fourier-Biot equation and provides the basic tool for heat conduction analysis. From its solution, we can obtain the temperature field as a function of time.
In words, the heat conduction equation states that:
At any point in the medium, the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume.
See also: Thermal Diffusivity
Example – Thermal Conduction in Fuel Rod
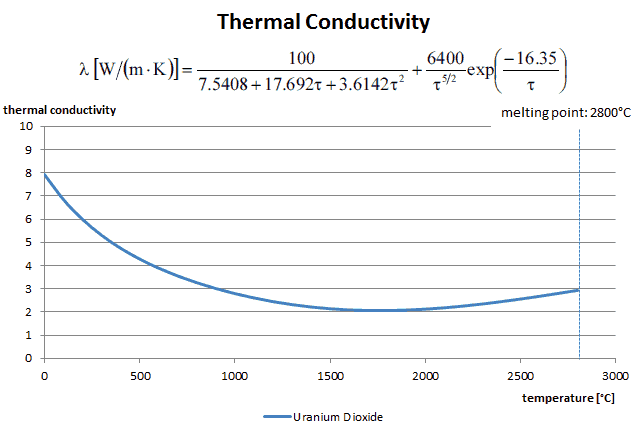
Most PWRs use uranium fuel, which is in the form of uranium dioxide. Uranium dioxide is a black semiconducting solid with very low thermal conductivity. On the other hand, uranium dioxide has a very high melting point and well-known behavior. The UO2 is pressed into cylindrical pellets, and these pellets are then sintered into the solid.
These cylindrical pellets are then loaded and encapsulated within a fuel rod (or fuel pin) made of zirconium alloys due to their very low absorption cross-section (unlike stainless steel). The surface of the tube, which covers the pellets, is called fuel cladding.
See also: Thermal Conduction of Uranium Dioxide
The thermal and mechanical behavior of fuel pellets and fuel rods constitute one of three key core design disciplines. Nuclear fuel is operated under inhospitable conditions (thermal, radiation, mechanical) and must withstand more than normal conditions operation. For example, temperatures in the center of fuel pellets reach more than 1000°C (1832°F), accompanied by fission-gas releases. Therefore detailed knowledge of temperature distribution within a single fuel rod is essential for the safe operation of nuclear fuel. This section will study the heat conduction equation in cylindrical coordinates using Dirichlet boundary conditions with given surface temperature (i.e., using Dirichlet boundary condition). Comprehensive analysis of fuel rod temperature profile will be studied in a separate section.
The temperature in the centerline of a fuel pellet
Consider the fuel pellet of radius rU = 0.40 cm, in which there is uniform and constant heat generation per unit volume, qV [W/m3]. Instead of volumetric heat rate qV [W/m3], engineers often use the linear heat rate, qL [W/m], representing the heat rate of one meter of the fuel rod. The linear heat rate can be calculated from the volumetric heat rate by:
The centreline is taken as the origin for r-coordinate. Due to symmetry in the z-direction and azimuthal direction, we can separate variables and simplify this problem to a one-dimensional problem. Thus, we will only solve for the temperature as a function of radius, T(r). For constant thermal conductivity, k, the appropriate form of the cylindrical heat equation, is:
The general solution of this equation is:
where C1 and C2 are the constants of integration.
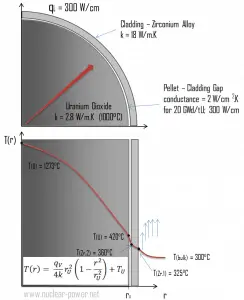Calculate the temperature distribution, T(r), in this fuel pellet, if:
- the temperature at the surface of the fuel pellet is TU = 420°C
- the fuel pellet radius rU = 4 mm.
- the averaged material’s conductivity is k = 2.8 W/m.K (corresponds to uranium dioxide at 1000°C)
- the linear heat rate is qL = 300 W/cm and thus the volumetric heat rate is qV = 597 x 106 W/m3
In this case, the surface is maintained at given temperatures TU. This corresponds to the Dirichlet boundary condition. Moreover, this problem is thermally symmetric, and therefore we may also use thermal symmetry boundary conditions. The constants may be evaluated using substitution into the general solution and are of the form:
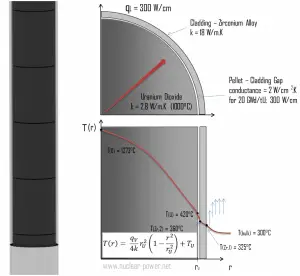
The resulting temperature distribution and the centerline (r = 0) temperature (maximum) in this cylindrical fuel pellet at these specific boundary conditions will be:
The radial heat flux at any radius, qr [W.m-1], in the cylinder may, of course, be determined by using the temperature distribution and with Fourier’s law. Note that, with heat generation, the heat flux is no longer independent of r.
∆T in fuel pellet
Detailed knowledge of geometry, the outer radius of fuel pellet, volumetric heat rate, and the pellet surface temperature (TU) determines ∆T between outer surface and centerline of fuel pellet. Therefore we can calculate the centerline temperature (TZr,2) simply using the energy conservation between heat generated in the volume and the transferred outside the volume:
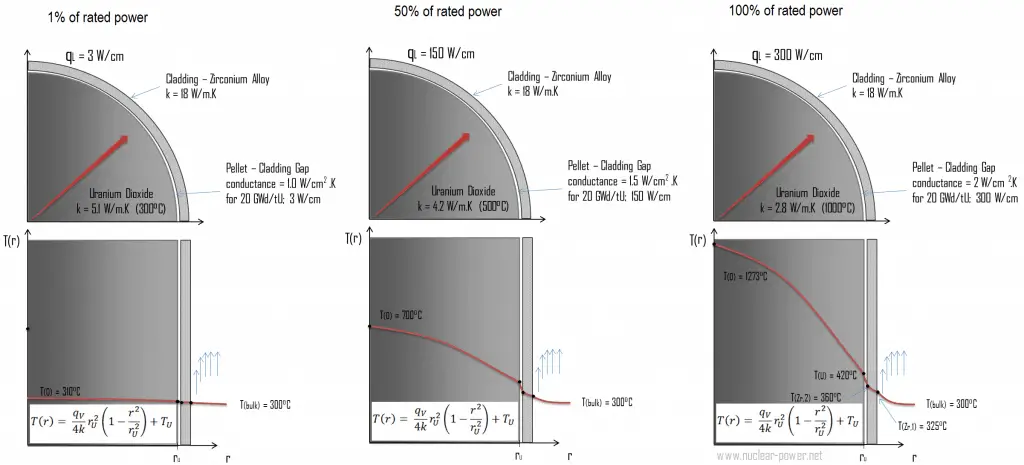
The following figure shows the temperature distribution in the fuel pellet at various power levels.
______
The temperature in an operating reactor varies from point to point within the system. Consequently, there is always one fuel rod and one local volume hotter than all the rest. The peak power limits must be introduced to limit these hot places. The peak power limits are associated with a boiling crisis and conditions that could cause fuel pellet melt. However, metallurgical considerations place upper limits on the temperature of the fuel cladding and the fuel pellet. Above these temperatures, there is a danger that the fuel may be damaged. One of the major objectives in the design of nuclear reactors is to provide for the removal of the heat produced at the desired power level while assuring that the maximum fuel temperature and the maximum cladding temperature are always below these predetermined values.
