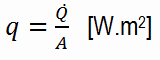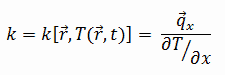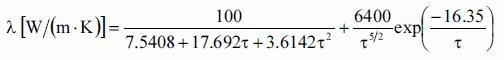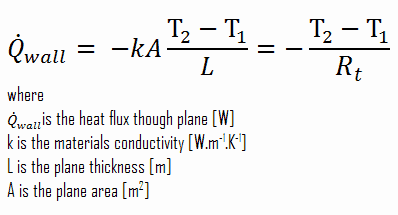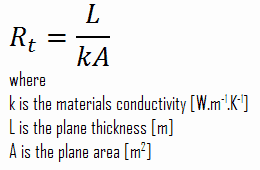Fourier’s law of thermal conduction law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area, at right angles to that gradient, through which the heat flows.
Heat transfer processes can be quantified in terms of appropriate rate equations. The rate equation in this heat transfer mode is based on Fourier’s law of thermal conduction. This law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area, at right angles to that gradient, through which the heat flows. Its differential form is:

Heat Flux
The
rate of heat transfer per unit area normal to the direction of heat transfer is called
heat flux. Sometimes it is also referred to as
heat flux density. In SI, its units are watts per square meter (W.m
−2). It has both a direction and a magnitude, so it is a vector quantity. The average heat flux is expressed as:
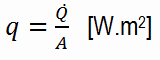
where A is the heat transfer area. The unit of heat flux in English units is Btu/h·ft2. Note that heat flux may vary with time and position on a surface.
In nuclear reactors, limitations of the local heat flux are of the highest importance for reactor safety. Since nuclear fuel consists of fuel rods, the heat flux is defined in units of W/cm (local linear heat flux) or kW/rod (power per fuel rod).
The proportionality constant obtained in the relation is known as
thermal conductivity,
k (or
λ), of the material. A material that readily transfers energy by conduction is a good thermal conductor and has a high value of
k.
Fourier’s law is an expression that defines
thermal conductivity.
As can be seen, solve Fourier’s law, we have to involve the temperature difference, the geometry, and the thermal conductivity of the object. This law was first formulated by Joseph Fourier in 1822, who concluded that “the heat flux resulting from thermal conduction is proportional to the magnitude of the temperature gradient and opposite to it in sign”.
Similarly, as Fourier’s law determines the heat flux through a slab, it can also be used to determine the temperature difference when q is known. This can be used to calculate the temperature in the center of the fuel pellet, as will be shown in the following sections.
Thermal Conductivity
The heat transfer characteristics of solid material are measured by a property called the
thermal conductivity, k (or λ), measured in
W/m.K. It measures a substance’s ability to transfer heat through a material by conduction. Note that
Fourier’s law applies to all matter, regardless of its state (solid, liquid, or gas). Therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature, and for vapors, it also depends upon pressure. In general:
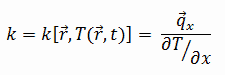
Most materials are nearly homogeneous. Therefore, we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material, the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
The previous equation follows that the conduction heat flux increases with increasing thermal conductivity and increases with increasing temperature differences. In general, the thermal conductivity of a solid is larger than that of a liquid, which is larger than that of a gas. This trend is due largely to differences in intermolecular spacing for the two states of matter. In particular, diamond has the highest hardness and thermal conductivity of any bulk material.
See also: Thermal Conductivity
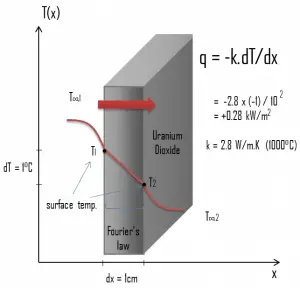
Thermal Conductivity of Uranium Dioxide
Most of
PWRs use
uranium fuel, which is in the form of
uranium dioxide. Uranium dioxide is a black semiconducting solid with
very low thermal conductivity. On the other hand, uranium dioxide has a
very high melting point and
well-known behavior. The UO2 is pressed into
pellets, and these pellets are then sintered into the solid.
These pellets are then loaded and encapsulated within a fuel rod (or fuel pin) made of zirconium alloys due to their very low absorption cross-section (unlike stainless steel). The surface of the tube, which covers the pellets, is called fuel cladding. Fuel rods are the base element of a fuel assembly.
The thermal conductivity of uranium dioxide is very low compared with metal uranium, uranium nitride, uranium carbide, and zirconium cladding material. Thermal conductivity is one of the parameters which determine the fuel centerline temperature. This low thermal conductivity can result in localized overheating in the fuel centerline, and therefore this overheating must be avoided. Overheating of the fuel is prevented by maintaining the steady-state peak linear heat rate (LHR) or the Heat Flux Hot Channel Factor – FQ(z) below the level at which fuel centerline melting occurs. Expansion of the fuel pellet upon centerline melting may cause the pellet to stress the cladding to the point of failure.
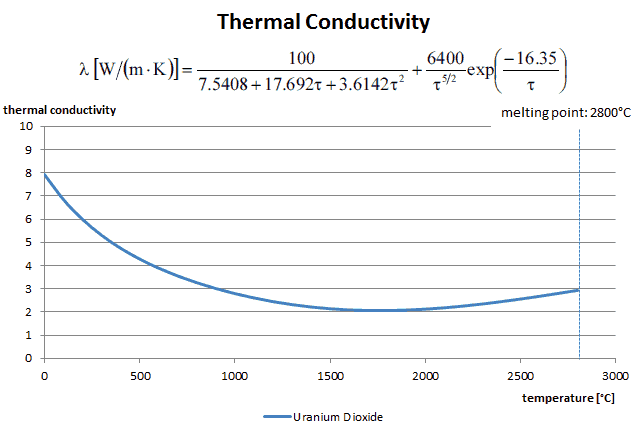
Thermal conductivity of solid UO2 with a density of 95% is estimated by the following correlation [Klimenko; Zorin]:
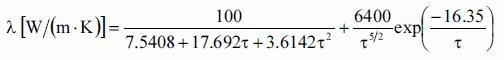
where τ = T/1000. The uncertainty of this correlation is +10% in the range from 298.15 to 2000 K and +20% in the range from 2000 to 3120 K.
Special reference: Thermal and Nuclear Power Plants/Handbook ed. by A.V. Klimenko and V.M. Zorin. MEI Press, 2003.
Special reference: Thermophysical Properties of Materials For Nuclear Engineering: A Tutorial and Collection of Data. IAEA-THPH, IAEA, Vienna, 2008. ISBN 978–92–0–106508–7.
Example – Heat flux through a window
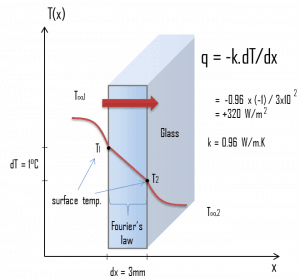 Heat loss through windows
Heat loss through windows
A major source of heat loss from a house is through the windows. Calculate the rate of heat flux through a glass window 1.5 m x 1.0 m in area and 3.0 mm thick if the temperatures at the inner and outer surfaces are 14.0°C and 13.0°C, respectively. Calculate the heat flux through this window.
Solution:
At this point, we know the temperatures at the surfaces of the material, and these temperatures are also given by conditions inside the house and outside the house. In this case, heat flows by conduction through the glass from the higher inside temperature to the lower outside temperature. We use the Fourier’s law of thermal conduction equation:

We assume that the thermal conductivity of a common glass is k = 0.96 W/m.K.
The heat flux will then be:
q = 0.96 [W/m.K] x 1 [K] / 3.0 x 10-3 [m] = 320 W/m2
The total heat loss through this window will be:
qloss = q . A = 320 x 1.5 x 1.0 = 480W
Fourier’s Law and Thermal Resistance
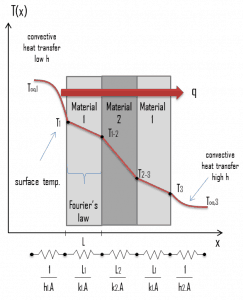 Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.
Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.
Consider a plane wall of thickness L and average thermal conductivity k. The two surfaces of the wall are maintained at constant temperatures of T1 and T2. For one-dimensional steady heat conduction through the wall, we have T(x). Then Fourier’s law of heat conduction for the wall can be expressed as:
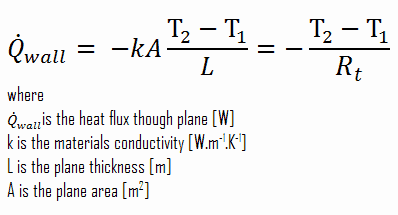
Thermal resistance is a heat property and a temperature difference measurement by which an object or material resists a heat flow. The thermal resistance for conduction in a plane wall is defined as:
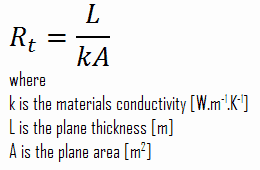
References:
Heat Transfer:
- Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
- U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
- Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.
See above:
Thermal Conduction
 Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.
Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.