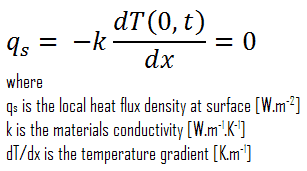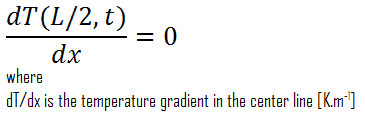Special Case – Adiabatic Boundary – Perfectly Insulated Boundary
A special case of this condition corresponds to the perfectly insulated surface for which (∂T/∂x = 0). Heat transfer through a properly insulated surface can be taken to be zero since adequate insulation reduces heat transfer through a surface to negligible levels. Mathematically, this boundary condition can be expressed as:
Special Case – Thermal Symmetry
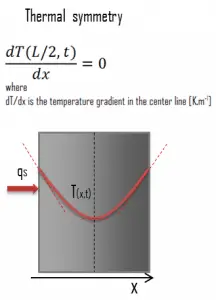 Another very important case that can be used for solving heat transfer problems involving fuel rods is thermal symmetry. For example, the two surfaces of a large hot plate of thickness L suspended vertically in the air will be subjected to the same thermal conditions. Thus, the temperature distribution will be symmetrical (i.e., one half of the plate will be the same temperature profile as the other half). As a result, there must be a maximum in the centerline of the plate, and the centerline can be viewed as an insulated surface (∂T/∂x = 0). The thermal condition at this plane of symmetry can be expressed as:
Another very important case that can be used for solving heat transfer problems involving fuel rods is thermal symmetry. For example, the two surfaces of a large hot plate of thickness L suspended vertically in the air will be subjected to the same thermal conditions. Thus, the temperature distribution will be symmetrical (i.e., one half of the plate will be the same temperature profile as the other half). As a result, there must be a maximum in the centerline of the plate, and the centerline can be viewed as an insulated surface (∂T/∂x = 0). The thermal condition at this plane of symmetry can be expressed as:
See also: Neumann Boundary Condition