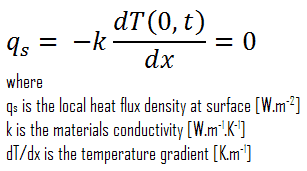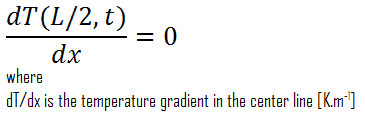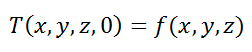As for another differential equation, the solution is given by boundary and initial conditions. Several common possibilities are simply expressed in the mathematical form concerning the boundary conditions.
Because the heat equation is second order in the spatial coordinates, two boundary conditions must be given for each direction of the coordinate system. Heat transfer is significant to describe a heat transfer problem completely. Therefore, we need to specify four boundary conditions for two-dimensional problems and six boundary conditions for three-dimensional problems.
Four kinds of boundary conditions commonly encountered in heat transfer are summarized in following section:
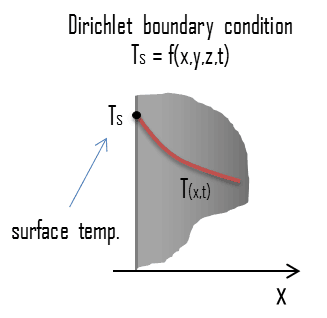In mathematics, the Dirichlet (or first-type) boundary condition is a type of boundary condition, named after a German mathematician Peter Gustav Lejeune Dirichlet (1805–1859). When imposed on an ordinary or a partial differential equation, the condition specifies the values in which the derivative of a solution is applied within the boundary of the domain.
This condition corresponds to a given fixed surface temperature in heat transfer problems. The Dirichlet boundary condition is closely approximated, for example, when the surface is in contact with a melting solid or a boiling liquid. In both cases, there is heat transfer at the surface, while the surface remains at the temperature of the phase change process.
In mathematics, the Neumann (or second-type) boundary condition is a type of boundary condition, named after a German mathematician Carl Neumann (1832–1925). When imposed on an ordinary or a partial differential equation, it specifies the values that a solution needs to take along the domain’s boundary.
In heat transfer problems, the Neumann condition corresponds to a given rate of change of temperature. In other words, this condition assumes that the heat flux at the material’s surface is known. The heat flux in the positive x-direction anywhere in the medium, including the boundaries, can be expressed by Fourier’s law of heat conduction.
Special Case – Adiabatic Boundary – Perfectly Insulated Boundary
A special case of this condition corresponds to the perfectly insulated surface for which (∂T/∂x = 0). Heat transfer through a properly insulated surface can be taken to be zero since adequate insulation reduces heat transfer through a surface to negligible levels. Mathematically, this boundary condition can be expressed as:
Special Case – Thermal Symmetry
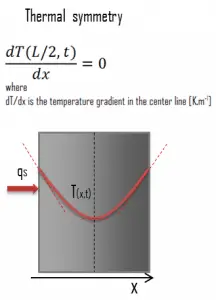Another very important case that can be used for solving heat transfer problems involving fuel rods is thermal symmetry. For example, the two surfaces of a large hot plate of thickness L suspended vertically in the air will be subjected to the same thermal conditions. Thus, the temperature distribution will be symmetrical (i.e., one half of the plate will be the same temperature profile as the other half). As a result, there must be a maximum in the centerline of the plate, and the centerline can be viewed as an insulated surface (∂T/∂x = 0). The thermal condition at this plane of symmetry can be expressed as:
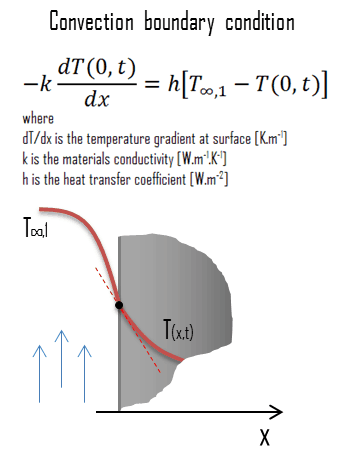In heat transfer problems, the convection boundary condition, also known as the Newton boundary condition, corresponds to the existence of convection heating (or cooling) at the surface and is obtained from the surface energy balance. Convection boundary condition is probably the most common boundary condition encountered in practice since most heat transfer surfaces are exposed to a convective environment at specified parameters.
In other words, this condition assumes that the heat conduction at the material’s surface is equal to the heat convection at the surface in the same direction. Since the boundary cannot store energy, the net heat entering the surface from the convective side must leave the surface from the conduction side.
Similarly, the radiation boundary condition can be constructed and used.
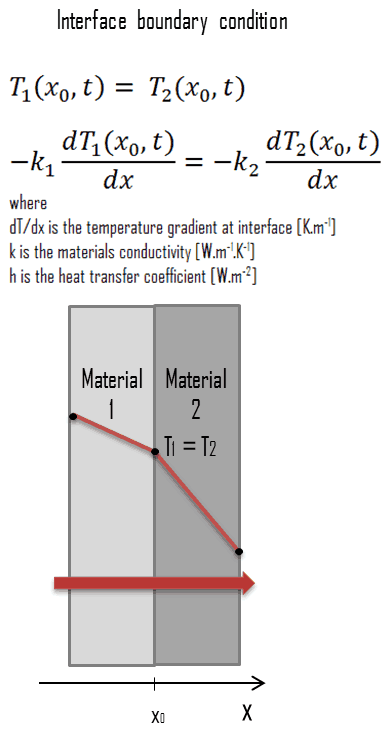In heat transfer problems, the interface boundary condition can be used when the material is made up of layers of different materials. The solution of a heat transfer problem in such a medium requires the solution of the heat transfer problem in each layer, and one must specify an interface condition at each interface. The interface boundary conditions at an interface are based on the two following requirements:
- two bodies in contact must have the same temperature at the area of contact (i.e., an ideal contact without contact resistance)
- an interface cannot store any energy, and therefore the heat conduction at the surface of the first material is equal to the heat conduction at the surface of the second material
Noteworthy, when components are bolted or otherwise pressed together, a knowledge of the thermal performance of such joints is also needed. The temperature drop across the interface between materials may be appreciable in these composite systems. This temperature drop is characterized by the thermal contact conductance coefficient, hc, which indicates the thermal conductivity, or ability to conduct heat, between two bodies in contact.
The interface boundary condition can be mathematically expressed in the way depicted in the figure.
where the function f(x, y, z) represents the temperature field inside the material at time t = 0. Note that under steady conditions, the heat conduction equation does not involve any time derivatives (∂T/∂t = 0), and thus we do not need to specify an initial condition.