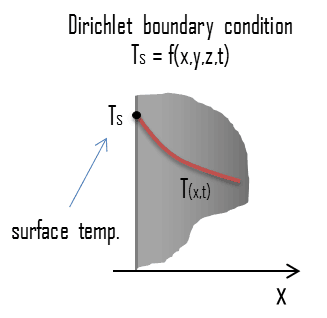
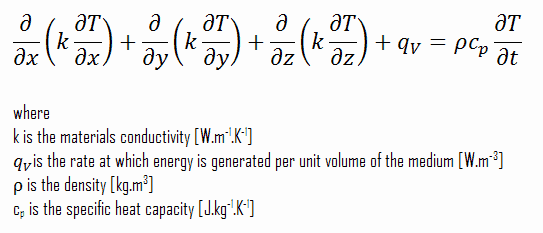In mathematics, the Dirichlet (or first-type) boundary condition is a type of boundary condition named after a German mathematician Peter Gustav Lejeune Dirichlet (1805–1859). When imposed on an ordinary or a partial differential equation, the condition specifies the values in which the derivative of a solution is applied within the domain’s boundary.
This condition corresponds to a given fixed surface temperature in heat transfer problems. The Dirichlet boundary condition is closely approximated, for example, when the surface is in contact with a melting solid or a boiling liquid. In both cases, there is heat transfer at the surface, while the surface remains at the temperature of the phase change process.
General Heat Conduction Equation
The heat conduction equation is a partial differential equation that describes heat distribution (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials. Once this temperature distribution is known, the conduction heat flux at any point in the material or on its surface may be computed from Fourier’s law.
The heat equation is derived from Fourier’s law and conservation of energy. Fourier’s law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and the area at right angles to that gradient through which the heat flows.
A change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. That is:
∆Q = ρ.cp.∆T
General Form
Using these two equations, we can derive the general heat conduction equation:
This equation is also known as the Fourier-Biot equation and provides the basic tool for heat conduction analysis. From its solution, we can obtain the temperature field as a function of time.
In words, the heat conduction equation states that:
At any point in the medium the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume.
