Facebook Instagram Youtube Twitter

Thermal Conductivity of Glass

Thermal Conductivity of Glass is about k = 1 W/m.K

Glass is a non-crystalline amorphous solid that is often transparent and has widespread practical, technological, and decorative usage in, for example, window panes. Glass is made of sand and other minerals that are melted together at very high temperatures to form a material that is ideal for a wide range of uses. Since it is an amorphous solid material, it has not had high thermal conductivity, and its thermal conductivity is about k = 1 W/m.K.

Example – Heat flux through a window

A major source of heat loss from a house is through the windows. Calculate the rate of heat flux through a glass window 1.5 m x 1.0 m in area and 3.0 mm thick if the temperatures at the inner and outer surfaces are 14.0°C and 13.0°C, respectively. Calculate the heat flux through this window.

Solution:

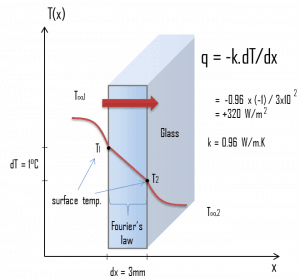Example - Heat Flux - Thermal ConductionAt this point, we know the temperatures at the surfaces of the material, and these temperatures are also given by conditions inside the house and outside the house. In this case, heat flows by conduction through the glass from the higher inside temperature to the lower outside temperature. We use the heat conduction equation:

Heat loss through window - equation

We assume that the thermal conductivity of a common glass is k = 0.96 W/m.K.

The heat flux will then be:

q = 0.96 [W/m.K] x 1 [K] / 3.0 x 10-3 [m] = 320 W/m2

The total heat loss through this window will be:

qloss = q . A = 320 x 1.5 x 1.0 = 480W

Thermal Conductivity of Nonmetals

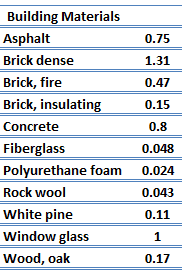thermal conductivity - building materialsFor nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. Lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass, at sufficiently high temperatures kph ∝ 1/T.

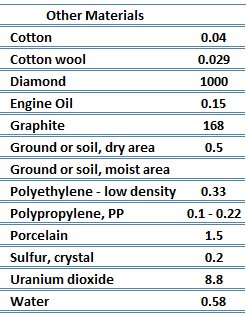thermal conductivity - solidsThe quanta of the crystal vibrational field are called ‘‘phonons.’’ A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Phonons play a major role in many of the physical properties of condensed matter, like thermal conductivity and electrical conductivity. In fact, for crystalline, nonmetallic solids such as diamond kph can be quite large, exceeding values of k associated with good conductors, such as aluminum. In particular, diamond has the highest hardness and thermal conductivity (k = 1000 W/m.K) of any bulk material.

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Thermal Conductivity